Факти про геометрію

Геометрія є одним з найважливіших розділів математики . Вона наочно дозволяє відобразити різні закономірності і геометричні об'єкти. Її виникнення цієї науки сягає в глиб віків і пов'язане з розвитком ремісничої справи, культури і мистецтва, а також низки нагальних практичних завдань (вимір земельних ділянок і об'ємів тіл).

Математика для древніх греків була, перш за все, геометрією. Тому над двері Академії, в стінах якої Платон вчив своїх учнів, висів напис: «Нехай сюди не входить той, хто не знає геометрії».

Трапеція - дуже відома геометрична фігура

Слово «трапеція» походить від давньогрецького слова «трапезіон» (позначає столик). також від даного слова відбулися вже трохи призабуті в побуті слова, такі як «трапеза» та інші споріднені з ним слова.

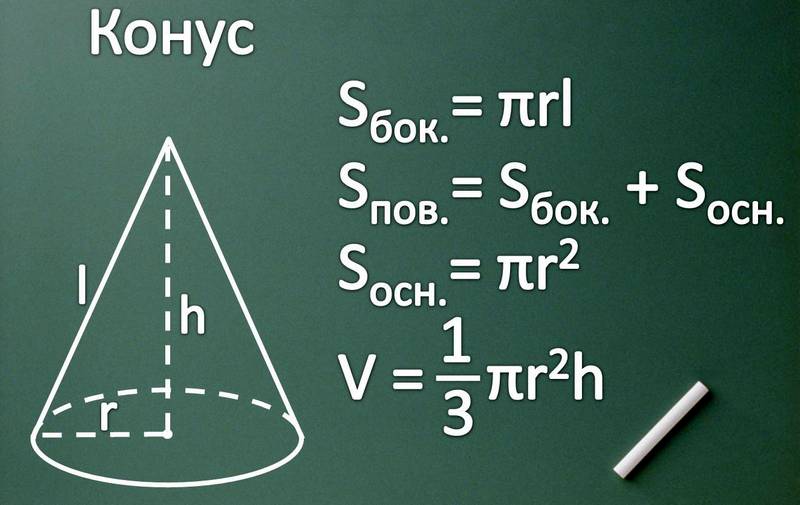Малюнок і формули конуса

Грецьке слово «Коносу», що позначає соснову шишку, є словникової основою для такого терміну як «конус», а відомий в геометрії термін «лінія» виник вже від латинського слова «лінум» (що в перекладі на російську мову означає «лляна нитка») .

Геометричні фігури

Серед всіх геометричних форм з однаковим периметром, коло має найбільшу площу і, навпаки, серед всіх фігур з однаковою площею коло має найменший периметр. «Квадратура кола» - це математична задача, яка полягає в геометричному побудові за допомогою циркуля і лінійки, квадрата, рівновеликого за площею даному колу. У 1882 році, Фердинандом Ліндеманн, була математично доведена нерозв'язність цієї задачі. однак це, не завадило багатьом людям продовжити витрачати свій час на її рішення. Так з'явилася відома всім метафора обумовлена ​​саме безперспективність подібних досліджень.

Як розрізати пиріг на 8 частин?

Пиріг розрізається всього трьома дотиками ножа на вісім рівних частин. Причому, існує тільки два способи це зробити.

Під трикутником Рело розуміють геометричну фігуру, утворену перетином 3 кіл однакового радіуса D з центрами, які знаходяться в вершинах рівностороннього трикутника, такий же по довжині боку. на основі трикутника Рело було придумано свердло, що дозволяє просвердлювати майже квадратні отвори.

Правило виведене знаменитим італійським вченим Леонардом да Вінчі свідчить, що квадрат діаметра (D) стовбура дерева дорівнює сумі квадратів діаметрів (d1 і d2) гілок, взятих на загальну фіксовану висоті. Пізніші дослідження підтвердили це твердження лише з одним застереженням - ступінь у формулі необов'язково має дорівнювати двом, а може лежати в діапазоні чисел від 1,8 до 2,3.

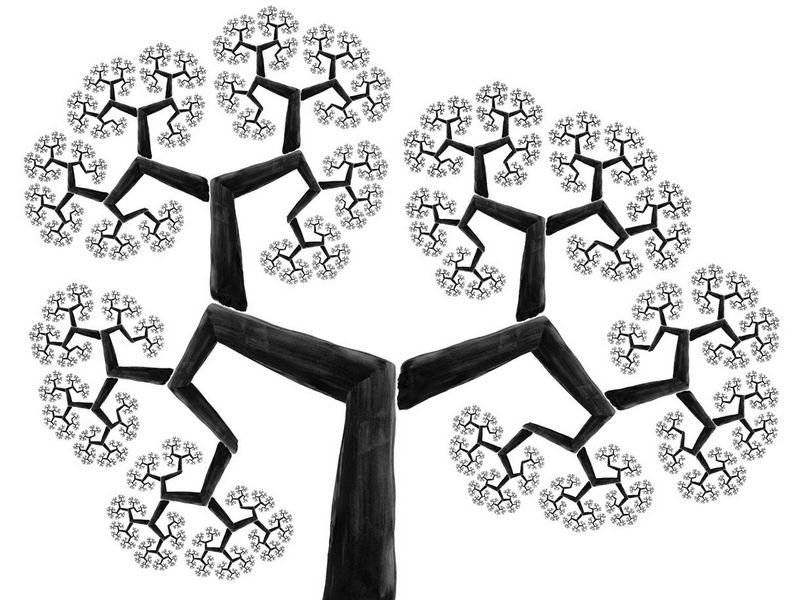Малюнок фрактального дерева

Спочатку вважалося, що така закономірність пояснюється тим, що для дерева з подібною структурою є більш оптимальний механізм постачання гілок поживними соками. Але, в 2010 році, американським фізиком Крістофом Еллою було придумано просте пояснення даному феномену. При розгляді дерева як фрактал, зменшується ймовірність зламу гілок під сильними поривами вітру.

Кут розташування листя один від одного може бути описаний дробом

Листя на гілках дерев, як стало відомо, завжди розташовуються в строго визначеному порядку. Вони відстоять один від одного на певний кут. Величина цього кута різна для різних рослин, однак, що найцікавіше, вона завжди описується простий дробом, де чисельник і знаменник представлені числами з ряду Фібоначчі. Наприклад, листя бука утворюють кут рівний 1/3, або 120 °, для дуба і абрикоса він представлений дробом 2/5, у груші і тополі - 3/8, у верби і мигдалю - 5/13 і т.д. Подібне розташування дає можливість листю більш ефективно витягати вологу і отримувати сонячне світло.

Качан капусти сорту Романеско

Красиві суцвіття капусти сорту Романеско є фрактали природного походження. Бутони цього сорту капусти описуються суворої логарифмічною спіраллю і складаються з більш дрібних бутонів, закручених за тим же принципом. Дана самоподібна структура повторюється ще кілька разів.

Вузли на мотузці

Майже 5000 років тому стародавні єгиптяни вже знали, що якщо зав'язати на мотузці дванадцять вузликів віддалених один від одного на однаковій відстані, а потім натягнути її в формі трикутника, то утворюється фігура з одним прямим кутом. Це знання допомагало робити правильну розмітку родючих земель в долині Нілу.

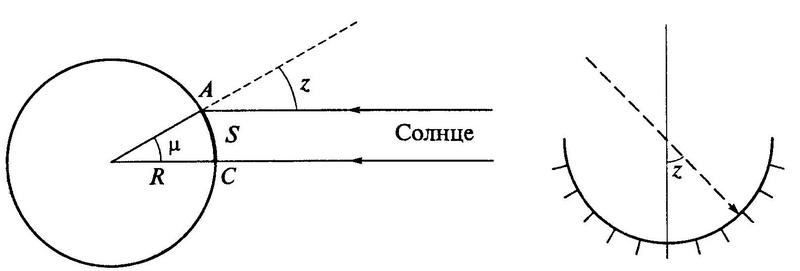Малюнок розрахунку довжини кола (меридіана) Землі

За допомогою геометричних правил і припущення про те, що наша земля куляста, давньогрецький вчений Ератосфен виміряв довжину її окружності. Їм було помічено, що, коли сонце знаходиться в Сієні (Африка) прямо над головою, в Олександрії, яка розташована від цього місця на 800 кілометрів, воно відхиляється від вертикалі на 7 °. Ератосфен уклав, що якщо з центру Землі Сонце видно під кутом 7 ° і, отже, окружність земної кулі дорівнює 360: 7 ° Х800 = 41 140 кілометрів.

Понад два тисячоліття Евклід, що дав особливо вдале і струнке виклад геометрії, був незаперечним законодавцем в цій області математики. Навіть німецький філософ Іманнуіл Кант вважав геометрію Евкліда єдино можливою. Однак були неясності в Евклідовому викладі геометрії, які не задовольняло математиків. Це єдинство паралельної до даної прямої, яку можна провести в площині через дану точку А. Евклід вважав це положення аксіомою, а деякі математики пізніше спробували довести цей факт, як теорему. Однак протягом століть доказів ніхто не знаходив.

Титульна сторінка з праці Н. І. Лобачевського

Цю загадку паралельності вирішив професор Казанського університету М. І. Лобачевський, який опублікував про своє відкриття в 1826 році. Трохи пізніше до подібних висновків дійшли німецький математик Карл Гаусс і угорський математик Янош Бояи. Обидва вчених встановили, що єдиність паралельної не можна довести в вигляді теореми. Наприклад, якщо допустити можливість провести через точку більше однієї прямої, що не перетинаються з даною, то ми прийдемо до іншого виду геометрії - неевклідової, в якій, цих протиріч спостерігатися не буде. Таку геометрію пізніше назвали геометрією Лобачевського.

В геометрії Лобачевського паралельні прямі не перетинаються один з одним в силу самого визначення паралельності. Основна відмінність геометрії Лобачевського від евклідової є положення, що через одну точку, що не лежить на даній прямій, можна провести не одну, а принаймні 2 цієї статті не перетинають її прямих, що знаходяться в тій же площині.

В геометрії Лобачевського сума всіх кутів трикутника менше 180 градусів. Два перпендикуляра виходять з однієї прямої все далі і далі будуть відходити одна від одної.