фрактал

  1. Самоподібні безлічі з незвичайними властивостями в математиці [ правити | правити код ]
  2. Рекурсивна процедура отримання фрактальних кривих [ правити | правити код ]
  3. Фрактали як нерухомі точки стискають відображень [ правити | правити код ]
  4. Фрактали в комплексній динаміці [ правити | правити код ]
  5. Стохастичні фрактали [ правити | правити код ]
  6. Природні об'єкти, що володіють фрактальними властивостями [ правити | правити код ]
  7. Природні науки [ правити | правити код ]
  8. Радіотехніка [ правити | правити код ]
  9. Інформатика [ правити | правити код ]
  10. Комп'ютерна графіка [ правити | правити код ]
  11. Децентралізовані мережі [ правити | правити код ]

фрактал ( лат. fractus - подрібнений, зламаний, розбитий) - безліч , Що володіє властивістю самоподібності (Об'єкт, в точності або приблизно збігається з частиною себе самого, тобто ціле має ту ж форму, що і одна або більше частин). У математиці під фракталами розуміють безлічі точок в евклідовому просторі , Що мають дробову метричну розмірність (в сенсі Маньківського або Хаусдорфа ), Або метричну розмірність, відмінну від топологічної , Тому їх слід відрізняти від інших геометричних фігур, обмежених кінцевим числом ланок. Самоподібні фігури, що повторюються кінцеве число раз, називаються предфракталамі.

Перші приклади самоподібних множин з незвичайними властивостями з'явилися в XIX столітті в результаті вивчення безперервних недіфференціруемих функцій (наприклад, функція Больцано , функція Вейєрштрасса , безліч Кантора ). Термін «фрактал» введений Бенуа Мандельброт в 1975 році і отримав широку популярність з виходом в 1977 році його книги « Фрактальна геометрія природи ». Особливу популярність фрактали знайшли з розвитком комп'ютерних технологій, що дозволили ефектно візуалізувати ці структури.

Слово «фрактал» вживається не тільки в якості математичного терміна. Фракталом може називатися предмет, що володіє, по крайней мере, одним із зазначених нижче властивостей:

  • Володіє нетривіальною структурою на всіх масштабах. У цьому відмінність від регулярних фігур (таких як окружність , еліпс , графік гладкої функції ): Якщо розглянути невеликий фрагмент регулярної фігури в дуже великому масштабі, то він буде схожий на фрагмент прямої. Для фрактала збільшення масштабу не веде до спрощення структури, тобто на всіх шкалах можна побачити однаково складну картину.
  • Є самоподібним або приблизно самоподібним.
  • Володіє дробової метричної розмірністю або метричної розмірністю, яка перевершує топологічну.

Багато об'єктів в природі мають властивості фрактала, наприклад: узбережжя, хмари, крони дерев, сніжинки, система кровообігу, альвеоли .

Самоподібні безлічі з незвичайними властивостями в математиці [ правити | правити код ]

Починаючи з кінця XIX століття, в математиці з'являються приклади самоподібних об'єктів з патологічними з точки зору класичного аналізу властивостями. До них можна віднести наступні:

Рекурсивна процедура отримання фрактальних кривих [ правити | правити код ]

існує проста рекурсивна процедура отримання фрактальних кривих на площині. Задамо довільну ламану з кінцевим числом ланок, звану генератором. Далі замінимо в ній кожен відрізок генератором (точніше, ламаної, подібної генератору). У вийшла ламаної знову замінимо кожен відрізок генератором. Продовжуючи до нескінченності, в межі отримаємо фрактальну криву. На малюнку праворуч наведені перший, другий і четвертий кроки цієї процедури для кривої Коха.

Прикладами таких кривих служать:

За допомогою схожої процедури виходить дерево Піфагора .

Фрактали як нерухомі точки стискають відображень [ правити | правити код ]

Властивість самоподібності можна математично строго виразити таким чином. Нехай ψ i, i = 1, ..., n {\ displaystyle \ psi _ {i}, \, i = 1, \ dots, n} Властивість самоподібності можна математично строго виразити таким чином - стискають відображення площині. Розглянемо наступне відображення на безлічі всіх компактних (Замкнутих і обмежених) підмножин площині: Ψ: K ↦ ∪ i = 1 n ψ i (K) {\ displaystyle \ Psi \ colon K \ mapsto \ cup _ {i = 1} ^ {n} \ psi _ {i} (K)}

Можна показати, що відображення Ψ {\ displaystyle \ Psi} Можна показати, що відображення Ψ {\ displaystyle \ Psi} є стискає відображенням на безлічі компактів з метрикою Хаусдорфа є стискає відображенням на безлічі компактів з метрикою Хаусдорфа . Отже, по теоремі Банаха , Це відображення має єдину нерухому точку. Ця нерухома точка і буде нашим фракталом.

Рекурсивна процедура отримання фрактальних кривих, описана вище, є окремим випадком даної конструкції. У ній все відображення ψ i, i = 1, ..., n {\ displaystyle \ psi _ {i}, \, i = 1, \ dots, n} Рекурсивна процедура отримання фрактальних кривих, описана вище, є окремим випадком даної конструкції - відображення подібності, а n {\ displaystyle n} - число ланок генератора.

для трикутника Серпінського n = 3 {\ displaystyle n = 3} для трикутника Серпінського n = 3 {\ displaystyle n = 3} і відображення ψ 1 {\ displaystyle \ psi _ {1}} , Ψ 2 {\ displaystyle \ psi _ {2}} , Ψ 3 {\ displaystyle \ psi _ {3}} - гомотетии з центрами в вершинах правильного трикутника і коефіцієнтом 1/2 і відображення ψ 1 {\ displaystyle \ psi _ {1}} , Ψ 2 {\ displaystyle \ psi _ {2}} , Ψ 3 {\ displaystyle \ psi _ {3}} - гомотетии з центрами в вершинах правильного трикутника і коефіцієнтом 1/2. Легко бачити, що трикутник Серпінського переходить в себе при відображенні Ψ {\ displaystyle \ Psi} .

У разі, коли відображення ψ i {\ displaystyle \ psi _ {i}} У разі, коли відображення ψ i {\ displaystyle \ psi _ {i}} - перетворення подібності з коефіцієнтами r i> 0 {\ displaystyle r_ {i}> 0} , розмірність s {\ displaystyle s} фрактала (при деяких додаткових технічних умов) може бути обчислена як рішення рівняння r 1 s + r 2 s + ⋯ + rns = 1 {\ displaystyle r_ {1} ^ {s} + r_ {2} ^ {s} + \ dots + r_ {n} ^ {s} = 1} - перетворення подібності з коефіцієнтами r i> 0 {\ displaystyle r_ {i}> 0} , розмірність s {\ displaystyle s} фрактала (при деяких додаткових технічних умов) може бути обчислена як рішення рівняння r 1 s + r 2 s + ⋯ + rns = 1 {\ displaystyle r_ {1} ^ {s} + r_ {2} ^ {s} + \ dots + r_ {n} ^ {s} = 1} . Так, для трикутника Серпінського отримуємо s = ln ⁡ 3 / ln ⁡ 2 {\ displaystyle s = \ ln 3 / \ ln 2} .

З тієї ж теоремі Банаха , Почавши з будь-якого компактного безлічі і застосовуючи до нього ітерації відображення Ψ {\ displaystyle \ Psi} З тієї ж теоремі Банаха , Почавши з будь-якого компактного безлічі і застосовуючи до нього ітерації відображення Ψ {\ displaystyle \ Psi} , Ми отримаємо послідовність компактів, що сходяться (в сенсі метрики Хаусдорфа) до нашого фракталу , Ми отримаємо послідовність компактів, що сходяться (в сенсі метрики Хаусдорфа) до нашого фракталу.

Фрактали в комплексній динаміці [ правити | правити код ]

Фрактали природним чином виникають при вивченні нелінійних динамічних систем . Найбільш вивчений випадок, коли динамічна система задається ітераціями многочлена або голоморфної функції комплексної змінної на площині. Перші дослідження в цій області відносяться до початку 20 століття і пов'язані з іменами Фату і Жюліа.

Нехай F (z) {\ displaystyle F (z)} Нехай F (z) {\ displaystyle F (z)} - многочлен, z 0 {\ displaystyle z_ {0}} - комплексне число - многочлен, z 0 {\ displaystyle z_ {0}} - комплексне число . Розглянемо наступну послідовність: z 0, z 1 = F (z 0), z 2 = F (F (z 0)) = F (z 1), z 3 = F (F (F (z 0))) = F (z 2),. . . {\ Displaystyle z_ {0}, z_ {1} = F (z_ {0}), z_ {2} = F (F (z_ {0})) = F (z_ {1}), z_ {3} = F (F (F (z_ {0}))) = F (z_ {2}), ...}

Нас цікавить поведінка цієї послідовності при прагненні n {\ displaystyle n} Нас цікавить поведінка цієї послідовності при прагненні n {\ displaystyle n} до нескінченності до нескінченності. Ця послідовність може:

  • прагнути до нескінченності,
  • прагнути до кінцевого межі,
  • демонструвати в межі циклічне поведінку, наприклад: z 1, z 2, z 3, z 1, z 2, z 3,. . . {\ Displaystyle z_ {1}, z_ {2}, z_ {3}, z_ {1}, z_ {2}, z_ {3}, ...}
  • вести себе хаотично, тобто не демонструвати жоден з трьох згаданих типів поведінки.

Безлічі значень z 0 {\ displaystyle z_ {0}} Безлічі значень z 0 {\ displaystyle z_ {0}} , Для яких послідовність демонструє один конкретний тип поведінки, а також безлічі точок біфуркації між різними типами, часто мають фрактальні властивості , Для яких послідовність демонструє один конкретний тип поведінки, а також безлічі точок біфуркації між різними типами, часто мають фрактальні властивості.

так, безліч Жюліа - безліч точок біфуркації для многочлена F (z) = z 2 + c {\ displaystyle F (z) = z ^ {2} + c} так, безліч Жюліа - безліч точок біфуркації для многочлена F (z) = z 2 + c {\ displaystyle F (z) = z ^ {2} + c} (Або інший схожою функції), тобто тих значень z 0 {\ displaystyle z_ {0}} , Для яких поведінка послідовності z n {\ displaystyle z_ {n}} може різко змінюватися при як завгодно малих змінах z 0 {\ displaystyle z_ {0}} (Або інший схожою функції), тобто тих значень z 0 {\ displaystyle z_ {0}} , Для яких поведінка послідовності z n {\ displaystyle z_ {n}} може різко змінюватися при як завгодно малих змінах z 0 {\ displaystyle z_ {0}} .

Інший варіант отримання фрактальних множин - введення параметра в многочлен F (z) {\ displaystyle F (z)} Інший варіант отримання фрактальних множин - введення параметра в многочлен F (z) {\ displaystyle F (z)} і розгляд безлічі тих значень параметра, при яких послідовність z n {\ displaystyle z_ {n}} демонструє певну поведінку при фіксованому z 0 {\ displaystyle z_ {0}} і розгляд безлічі тих значень параметра, при яких послідовність z n {\ displaystyle z_ {n}} демонструє певну поведінку при фіксованому z 0 {\ displaystyle z_ {0}} . так, безліч Мандельброта - це безліч всіх c ∈ C {\ displaystyle c \ in \ mathbb {C}} , При яких z n {\ displaystyle z_ {n}} для F (z) = z 2 + c {\ displaystyle F (z) = z ^ {2} + c} і z 0 {\ displaystyle z_ {0}} не прагне до нескінченності.

Ще один відомий приклад такого роду - басейни Ньютона .

Популярно створення красивих графічних образів на основі комплексної динаміки шляхом розфарбовування точок площини в залежності від поведінки відповідних динамічних систем. Наприклад, для доповнення безлічі Мандельброта можна розфарбувати точки в залежності від швидкості прагнення z n {\ displaystyle z_ {n}} Популярно створення красивих графічних образів на основі комплексної динаміки шляхом розфарбовування точок площини в залежності від поведінки відповідних динамічних систем до нескінченності (яка визначається, скажімо, як найменший номер n {\ displaystyle n} , При якому | z n | {\ Displaystyle | z_ {n} |} перевищить фіксовану велику величину A {\ displaystyle A} ).

біоморфи - фрактали, побудовані на основі комплексної динаміки і нагадують живі організми.

Стохастичні фрактали [ правити | правити код ]

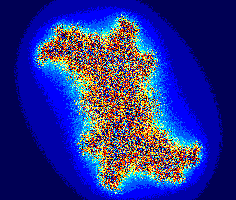
Рандомізований фрактал на основі безлічі Жюліа

Природні об'єкти часто мають фрактальну форму. Для їх моделювання можуть застосовуватися стохастичні (випадкові) фрактали. Приклади стохастичних фракталів:

  • траєкторія броунівського руху на площині і в просторі;
  • межа траєкторії броунівського руху на площині. У 2001 році Лоулер, Шрамм і Вернер довели припущення Мандельброта про те, що її розмірність дорівнює 4/3.
  • еволюції Шрамм-Лёвнера - конформно-інваріантні фрактальні криві, що виникають в критичних двовимірних моделях статистичної механіки , наприклад, в моделі Ізінга і перколяції .
  • різні види рандомізованих фракталів, тобто фракталів, отриманих за допомогою рекурсивної процедури, в яку на кожному кроці введений випадковий параметр. плазма - приклад використання такого фрактала в комп'ютерній графіці.

Природні об'єкти, що володіють фрактальними властивостями [ правити | правити код ]

Природні об'єкти (квазіфрактали) відрізняються від ідеальних абстрактних фракталів неповнотою і неточністю повторень структури. Більшість зустрічаються в природі фракталоподобних структур (межі хмар, лінія берега, дерева, листя рослин, корали , ...) є квазіфракталамі, оскільки на деякому малому масштабі фрактальна структура зникає. Природні структури не можуть бути ідеальними фракталами через обмеження, що накладаються розмірами живої клітини і, в кінцевому підсумку, розмірами молекул .

  • У живій природі:
  • У неживій природі:

Природні науки [ правити | правити код ]

У фізиці фрактали природним чином виникають при моделюванні нелінійних процесів, таких як турбулентний Протягом рідини, складні процеси дифузії - адсорбції , Полум'я, хмари тощо. Фрактали використовуються при моделюванні пористих матеріалів, наприклад, в нафтохімії. У біології вони застосовуються для моделювання популяцій і для опису систем внутрішніх органів (система кровоносних судин). Після створення кривої Коха було запропоновано використовувати її при обчисленні довжини берегової лінії.

Радіотехніка [ правити | правити код ]

Фрактальні антени [ правити | правити код ]

Використання фрактальної геометрії при проектуванні антенних пристроїв було вперше застосовано американським інженером Натаном Коеном, який тоді жив у центрі Бостона , Де була заборонена установка зовнішніх антен на будівлі. Натан вирізав з алюмінієвої фольги фігуру в формі кривої Коха і наклеїв її на аркуш паперу, потім приєднав до приймача .

Коен заснував власну компанію і налагодив серійний випуск своїх антен. C тих пір теорія фрактальних антен продовжує інтенсивно розвиватися. [1] [2] [3] Перевагою таких антен є багатодіапазонними і порівняльна широкополосность.

Інформатика [ правити | правити код ]

Стиснення зображень [ правити | правити код ]

Існують алгоритми стиснення зображення за допомогою фракталів. Вони засновані на ідеї про те, що замість самого зображення можна зберігати стискуюче відображення , Для якого це зображення (або деякий близьке до нього) є нерухомою точкою . Один з варіантів даного алгоритму був використаний [4] фірмою Microsoft при виданні своєї енциклопедії, але великого поширення ці алгоритми не отримали.

Комп'ютерна графіка [ правити | правити код ]

Ще одне фрактальное дерево

Фрактали широко застосовуються в комп'ютерній графіці для побудови зображень природних об'єктів, таких як дерева, кущі, гірські ландшафти, поверхні морів і так далі. Існує безліч програм, що служать для генерації фрактальних зображень, див. Генератор фракталів (програма) .

Децентралізовані мережі [ правити | правити код ]

Система призначення IP-адрес в мережі Netsukuku використовує принцип фрактального стиснення інформації для компактного збереження інформації про вузли мережі. Кожен вузол мережі Netsukuku зберігає всього 4 Кб інформації про стан сусідніх вузлів, при цьому будь-який новий вузол підключається до загальної мережі без необхідності в центральному регулюванні роздачі IP-адрес , Що, наприклад, характерно для мережі Інтернет. Таким чином, принцип фрактального стиснення інформації гарантує повністю децентралізовану, а отже, максимально стійку роботу всієї мережі.

  1. ↑ Вишневський В. М., Ляхов А. І., Кравець С. Л., Шахновіч І. В. Широкосмугові бездротові мережі передачі інформації. - М .: Техносфера. - 2005.- C. 498-569
  2. ↑ Крупенін С. В. Фрактальні випромінюють структури і аналогова модель фрактального імпедансу. Дис. канд. фіз.-мат. наук: 01.04.03, 01.04.04 / [Місце захисту: Моск. держ. ун-т ім. М. В. Ломоносова. Фіз. фак.] .- Москва, 2009.- 157 с.
  3. ↑ Бабічев Д. А. Розробка і дослідження мікрополоскової антени на основі фрактального підходу. Дис. канд. техн. наук: - 05.12.07. [Місце захисту: С.-Петерб. держ. електротехн. ун-т (ЛЕТІ)]. - Санкт-Петербург, 2016. - 104 с. [1]
  4. ↑ Фрактальное стиснення зображень на Computerworld Росія
  • А. А. Кирилов. Повість про двох фракталах . - Літня школа «Сучасна математика». - Дубна, 2007.
  • Мандельброт Б. Фрактальна геометрія природи. - М .: «Інститут комп'ютерних досліджень», 2002..
  • Пайтген Х.-О., Ріхтер П. Х. Краса фракталів. Образи комплексних динамічних систем. - М .: «Світ», 1993.
  • Федер Е. Фрактали. - М: «Мир», 1991.
  • Абачи С. К. Про трикутнику Паскаля, простих делителях і фрактальних структурах // Світ науки, 1989, № 9.
  • Фоменко А. Т. Наочна геометрія і топологія. - М .: изд-во МГУ, 1993.
  • Ціцін Ф. А. фрактальна всесвіт // «Дельфис» - № 11 (3) - 1997.
  • Фрактали у фізиці. Праці 6-го міжнародного симпозіуму по фракталам у фізиці, 1985. - М .: «Мир», 1988.
  • Маврікіді Ф. І. Фрактали: осягаючи взаємопов'язаний світ // «Дельфис» - № 23 (3) - 2000.
  • Шредер М. Фрактали, хаос, статечні закони. Мініатюри з нескінченного раю. - Іжевськ: «РГД», 2001.
  • Кроновер Р. М. Фрактали і хаос в динамічних системах. Основи теорії.
  • Мандельброт Бенуа , Річард Л. Хадсон. (Не) слухняні ринки: фрактальна революція у фінансах = The Misbehavior of Markets. - М.: «Вільямс» , 2006. - 400 с. - ISBN 5-8459-0922-8 .
  • Красиве життя комплексних чисел // Hard'n'Soft, № 9, 2002. Стор. 90.
  • М. Г. Іванов, « Розмір і розмірність »//« Потенціал », август 2006.
  • Маврікіді Ф. І. Фрактальна математика і природа змін // «Дельфис» - № 54 (2) - 2008.
  • Липів А. Н. Фрактали. Пам'яті Бенуа Мандельброта // Філософія і культура № 9 (33) 2010. № 8. С. 39-54.