Математична статистика
зміст
Вступ
1. Предмет і методи математичної статистики
2. Основні поняття математичної статистики
2.1 Основні поняття вибіркового методу
2.2 Вибіркове розподіл
2.3 Емпірична функція розподілу, гістограма
висновок
Список літератури
Вступ
Математична статистика - наука про математичні методи систематизації та використання статистичних даних для наукових і практичних висновків. У багатьох своїх розділах математична статистика спирається на теорію ймовірностей, що дозволяє оцінити надійність і точність висновків, зроблених на підставі обмеженого статистичного матеріалу (напр., Оцінити необхідний обсяг вибірки для отримання результатів необхідної точності при вибірковому обстеженні).
У теорії ймовірностей розглядаються випадкові величини із заданим розподілом або випадкові експерименти, властивості яких повністю відомі. Предмет теорії ймовірностей - властивості і взаємозв'язки цих величин (розподілів).
Але часто експеримент являє собою чорний ящик, який видає тільки деякі результати, за якими потрібно зробити висновок про властивості самого експерименту. Спостерігач має набір числових (або їх можна зробити числовими) результатів, отриманих повторенням одного і того ж випадкового експерименту в однакових умовах.
При цьому виникають, наприклад, такі питання: Якщо ми спостерігаємо одну випадкову величину - як по набору її значень в декількох дослідах зробити якомога точніший висновок про її розподілі?
Прикладом такої серії експериментів може служити соціологічне опитування, набір економічних показників або, нарешті, послідовність гербів і решек при тисячократно підкиданні монети.
Всі вищенаведені фактори обумовлюють актуальність і значимість тематики роботи на сучасному етапі, спрямованої на глибоке і всебічне вивчення основних понять математичної статистики.
У зв'язку з цим метою даної роботи є систематизація, накопичення і закріплення знань про поняття математичної статистики.
1. Предмет і методи математичної статистики
Математична статистика - наука про математичні методи аналізу даних, отриманих при проведенні масових спостережень (вимірювань, дослідів). Залежно від математичної природи конкретних результатів спостережень статистика математична ділиться на статистику чисел, багатовимірний статистичний аналіз, аналіз функцій (процесів) і тимчасових рядів, статистику об'єктів нечислової природи. Істотна частина статистики математичної заснована на імовірнісних моделях. Виділяють загальні завдання опису даних, оцінювання та перевірки гіпотез. Розглядають і більш приватні завдання, пов'язані з проведенням вибіркових обстежень, відновленням залежностей, побудовою і використанням класифікацій (типологій) і ін.
Для опису даних будують таблиці, діаграми, інші наочні уявлення, наприклад, кореляційні поля. Імовірнісні моделі зазвичай не застосовуються. Деякі методи опису даних спираються на просунуту теорію і можливості сучасних комп'ютерів. До них відносяться, зокрема, кластер-аналіз, націлений на виділення груп об'єктів, схожих один на одного, і багатовимірне шкалювання, що дозволяє наочно уявити об'єкти на площині, в найменшій мірі спотворивши відстані між ними.
Методи оцінювання та перевірки гіпотез спираються на імовірнісні моделі породження даних. Ці моделі діляться на параметричні і непараметричні. У параметричних моделях передбачається, що досліджувані об'єкти описуються функціями розподілу, що залежать від невеликого числа (1-4) числових параметрів. У непараметрических моделях функції розподілу передбачаються довільними безперервними. У статистиці математичної оцінюють параметри і характеристики розподілу (математичне очікування, медіану, дисперсію, квантилі і ін.), Щільності та функції розподілу, залежності між змінними (на основі лінійних і непараметричних коефіцієнтів кореляції, а також параметричних або непараметричних оцінок функцій, що виражають залежності) і ін. Використовують точкові і інтервальні (дають кордону для істинних значень) оцінки.
У математичній статистиці є загальна теорія перевірки гіпотез і велике число методів, присвячених перевірці конкретних гіпотез. Розглядають гіпотези про значення параметрів і характеристик, про перевірку однорідності (тобто про збіг характеристик або функцій розподілу в двох вибірках), про згоду емпіричної функції розподілу із заданою функцією розподілу або з параметричних сімейством таких функцій, про симетрії розподілу і ін.
Велике значення має розділ математичної статистики, пов'язаний з проведенням вибіркових обстежень, з властивостями різних схем організації вибірок і побудовою адекватних методів оцінювання і перевірки гіпотез.
Завдання відновлення залежностей активно вивчаються понад 200 років, з моменту розробки К. Гауссом в 1794 р методу найменших квадратів. В даний час найбільш актуальні методи пошуку інформативного підмножини змінних і непараметричні методи.
Розробка методів апроксимації даних і скорочення розмірності опису була розпочата більше 100 років тому, коли К. Пірсон створив метод головних компонент. Пізніше були розроблені факторний аналіз [1] і численні нелінійні узагальнення.
Різні методи побудови (кластер-аналіз), аналізу і використання (дискримінантний аналіз) класифікацій (типологій) називають також методами розпізнавання образів (з учителем і без), автоматичної класифікації та ін.
Математичні методи в статистиці засновані або на використання сум (на основі Центральної Граничною Теореми теорії ймовірностей) або показників відмінності (відстаней, метрик), як в статистиці об'єктів нечислової природи. Строго обгрунтовані зазвичай лише асимптотичні результати. В даний час комп'ютери відіграють велику роль в математичній статистиці. Вони використовуються як для розрахунків, так і для імітаційного моделювання (зокрема, в методах розмноження вибірок і при вивченні придатності асимптотичних результатів).
2. Основні поняття математичної статистики 2.1 Основні поняття вибіркового методу
нехай  - випадкова величина, яка спостерігається у випадковому експерименті. Передбачається, що імовірнісний простір задано (і не буде нас цікавити).
- випадкова величина, яка спостерігається у випадковому експерименті. Передбачається, що імовірнісний простір задано (і не буде нас цікавити).
Будемо вважати, що, провівши 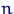 раз цей експеримент в однакових умовах, ми отримали числа
раз цей експеримент в однакових умовах, ми отримали числа 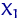 ,
, 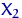 ,
,  ,
, 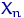 - значення цієї випадкової величини в першому, другому, і т.д. експериментах. Випадкова величина
- значення цієї випадкової величини в першому, другому, і т.д. експериментах. Випадкова величина 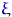 має деякий розподіл
має деякий розподіл  , Яке нам частково або повністю невідомо.
, Яке нам частково або повністю невідомо.
Розглянемо докладніше набір 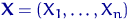 , Званий вибіркою.
, Званий вибіркою.
У серії вже вироблених експериментів вибірка - це набір чисел. Але якщо цю серію експериментів повторити ще раз, то замість цього набору ми отримаємо новий набір чисел. замість числа 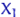 з'явиться інше число - одне зі значень випадкової величини
з'явиться інше число - одне зі значень випадкової величини 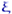 . Тобто
. Тобто 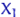 (і
(і 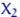 , і
, і  , І т.д.) - змінна величина, яка може приймати ті ж значення, що і випадкова величина
, І т.д.) - змінна величина, яка може приймати ті ж значення, що і випадкова величина 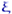 , І так само часто (з тими ж можливостями). Тому до досвіду
, І так само часто (з тими ж можливостями). Тому до досвіду 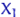 - випадкова величина, однаково розподілена з
- випадкова величина, однаково розподілена з 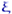 , А після досвіду - число, яке ми спостерігаємо в даному першому експерименті, тобто одне з можливих значень випадкової величини
, А після досвіду - число, яке ми спостерігаємо в даному першому експерименті, тобто одне з можливих значень випадкової величини 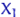 .
.
вибірка 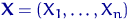 обсягу
обсягу  - це набір з
- це набір з  незалежних і однаково розподілених випадкових величин ( «копій
незалежних і однаково розподілених випадкових величин ( «копій 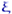 »), Що мають, як і
»), Що мають, як і 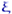 , розподіл
, розподіл  .
.
Що значить «по вибірці зробити висновок про розподіл»? Розподіл характеризується функцією розподілу, щільністю або таблицею, набором числових характеристик -  ,
,  ,
,  і т.д. За вибіркою потрібно вміти будувати наближення для всіх цих характеристик.
і т.д. За вибіркою потрібно вміти будувати наближення для всіх цих характеристик.
2.2 Вибіркове розподіл
Розглянемо реалізацію вибірки на одному елементарному кінець 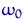 - набір чисел
- набір чисел 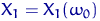 ,
,  ,
, 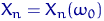 . На відповідному імовірнісному просторі введемо випадкову величину
. На відповідному імовірнісному просторі введемо випадкову величину 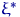 , Приймаючу значення
, Приймаючу значення 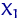 ,
,  ,
, 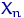 з вірогідністю по
з вірогідністю по 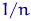 (Якщо якісь із значень збіглися, складемо вірогідність відповідне число раз). Таблиця розподілу ймовірностей і функція розподілу випадкової величини
(Якщо якісь із значень збіглися, складемо вірогідність відповідне число раз). Таблиця розподілу ймовірностей і функція розподілу випадкової величини 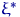 виглядають так:
виглядають так:

розподіл величини 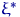 називають емпіричним або вибірковим розподілом. Обчислимо математичне сподівання і дисперсію величини
називають емпіричним або вибірковим розподілом. Обчислимо математичне сподівання і дисперсію величини 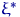 і введемо позначення для цих величин:
і введемо позначення для цих величин:
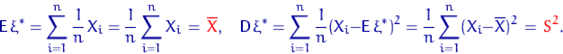
Точно так же обчислимо і момент порядку 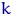
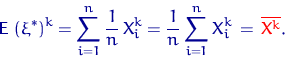
У загальному випадку позначимо через 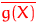 величину
величину
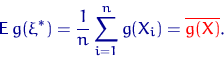
Якщо при побудові всіх введених нами характеристик вважати вибірку 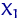 ,
,  ,
, 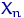 набором випадкових величин, то і самі ці характеристики -
набором випадкових величин, то і самі ці характеристики - 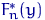 ,
,  ,
, 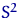 ,
, 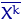 ,
, 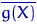 - стануть величинами випадковими. Ці характеристики вибіркового розподілу використовують для оцінки (наближення) відповідних невідомих характеристик істинного розподілу.
- стануть величинами випадковими. Ці характеристики вибіркового розподілу використовують для оцінки (наближення) відповідних невідомих характеристик істинного розподілу.
Причина використання характеристик розподілу 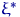 для оцінки характеристик істинного розподілу
для оцінки характеристик істинного розподілу 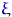 (або
(або 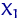 ) - в близькості цих розподілів при великих
) - в близькості цих розподілів при великих 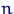 .
.
Розглянемо, для прикладу,  підкидань правильного кубика. нехай
підкидань правильного кубика. нехай 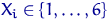 - кількість очок, що випали при
- кількість очок, що випали при 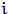 -м кидку,
-м кидку,  . Припустимо, що одиниця в вибірці зустрінеться
. Припустимо, що одиниця в вибірці зустрінеться  раз, двійка -
раз, двійка -  раз і т.д. Тоді випадкова величина
раз і т.д. Тоді випадкова величина  буде приймати значення 1,
буде приймати значення 1,  , 6 з вірогідністю
, 6 з вірогідністю 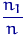 ,
,  ,
, 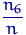 відповідно. Але ці пропорції з зростанням
відповідно. Але ці пропорції з зростанням  наближаються до
наближаються до 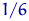 відповідно до закону великих чисел. Тобто розподіл величини
відповідно до закону великих чисел. Тобто розподіл величини  в деякому сенсі зближується з істинним розподілом числа очок, що випадають при підкиданні правильного кубика.
в деякому сенсі зближується з істинним розподілом числа очок, що випадають при підкиданні правильного кубика.
Ми не станемо уточнювати, що мається на увазі під близькістю вибіркового і істинного розподілів. У наступних параграфах ми докладніше познайомимося з кожної з введених вище характеристик і досліджуємо її властивості, в тому числі її поведінку з ростом обсягу вибірки.
2.3 Емпірична функція розподілу, гістограма
Оскільки невідоме розподіл 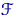 можна описати, наприклад, його функцією розподілу
можна описати, наприклад, його функцією розподілу 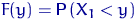 , Побудуємо за вибіркою «оцінку» для цієї функції.
, Побудуємо за вибіркою «оцінку» для цієї функції.
Визначення 1.
Емпіричної функцією розподілу, побудованої за вибіркою 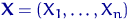 обсягу
обсягу 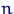 , Називається випадкова функція
, Називається випадкова функція  , При кожному
, При кожному 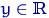 рівна
рівна
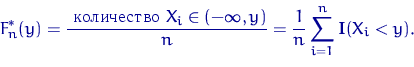
Нагадування: Випадкова функція
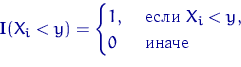
називається індикатором події 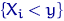 . при кожному
. при кожному 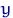 це - випадкова величина, що має розподіл Бернуллі з параметром
це - випадкова величина, що має розподіл Бернуллі з параметром  . чому?
. чому?
Інакше кажучи, при будь-якому 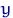 значення
значення 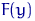 , Рівне істинної ймовірності випадкової величини
, Рівне істинної ймовірності випадкової величини 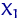 бути менше
бути менше 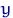 , Оцінюється часткою елементів вибірки, менших
, Оцінюється часткою елементів вибірки, менших 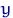 .
.
Якщо елементи вибірки 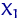 ,
,  ,
, 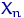 упорядкувати за зростанням (на кожному елементарному кінець), вийде новий набір випадкових величин, званий варіаційним рядом:
упорядкувати за зростанням (на кожному елементарному кінець), вийде новий набір випадкових величин, званий варіаційним рядом:

тут
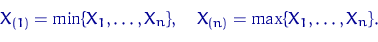
елемент 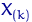 ,
, 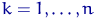 , називається
, називається 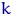 -м членом варіаційного ряду або
-м членом варіаційного ряду або 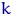 -й порядкової статистикою.
-й порядкової статистикою.
Приклад 1.
вибірка: 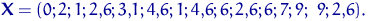
Варіаційний ряд: 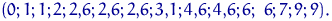
Мал. 1. Приклад 1
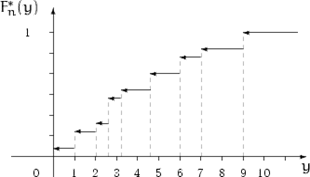
Емпірична функція розподілу має скачки в точках вибірки, величина стрибка в точці 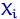 дорівнює
дорівнює 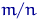 , де
, де  - кількість елементів вибірки, які збігаються з
- кількість елементів вибірки, які збігаються з 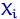 .
.
Можна побудувати емпіричну функцію розподілу по вариационному ряду:
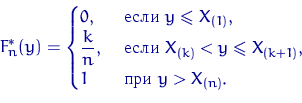
Іншою характеристикою розподілу є таблиця (для дискретних розподілів) або щільність (для абсолютно неперервних). Емпіричним, або вибірковим аналогом таблиці або щільності є так звана гістограма.
Гістограма будується по групованим даними. Передбачувану область значень випадкової величини 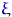 (Або область вибіркових даних) ділять незалежно від вибірки на кілька інтервалів (не обов'язково однакових). нехай
(Або область вибіркових даних) ділять незалежно від вибірки на кілька інтервалів (не обов'язково однакових). нехай 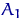 ,
,  ,
, 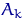 - інтервали на прямий, звані інтервалами угруповання. позначимо для
- інтервали на прямий, звані інтервалами угруповання. позначимо для 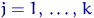 через
через 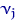 число елементів вибірки, що потрапили в інтервал
число елементів вибірки, що потрапили в інтервал 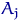 :
:
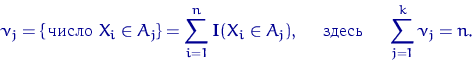
(1)
На кожному з інтервалів 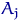 будують прямокутник, площа якого пропорційна
будують прямокутник, площа якого пропорційна 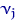 . Загальна площа всіх прямокутників повинна дорівнювати одиниці. нехай
. Загальна площа всіх прямокутників повинна дорівнювати одиниці. нехай 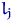 - довжина інтервалу
- довжина інтервалу 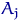 . Висота
. Висота 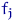 прямокутника над
прямокутника над 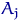 дорівнює
дорівнює
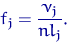
Отримана фігура називається гістограмою.
Приклад 2.
Є варіаційний ряд (див. Приклад 1):
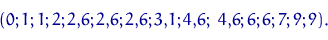
розіб'ємо відрізок 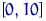 на 4 рівних відрізка. У відрізок
на 4 рівних відрізка. У відрізок 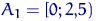 потрапили 4 елементи вибірки, в
потрапили 4 елементи вибірки, в 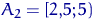 - 6, в
- 6, в 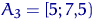 - 3, і в відрізок
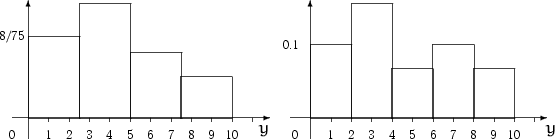
- 3, і в відрізок 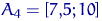 потрапили 2 елементи вибірки. Будуємо гістограму (рис. 2). На рис. 3 - теж гістограма для тієї ж вибірки, але при розбитті області на 5 рівних відрізків.
потрапили 2 елементи вибірки. Будуємо гістограму (рис. 2). На рис. 3 - теж гістограма для тієї ж вибірки, але при розбитті області на 5 рівних відрізків.
Мал. 2. Приклад 2
Мал. 3. Приклад 2
Зауваження 1.
В курсі «Економетрика» стверджується, що найкращим числом інтервалів угруповання ( «формула Стерджесс») є 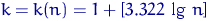 .
.
тут 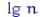 - десятковий логарифм, тому
- десятковий логарифм, тому  , Тобто при збільшенні вибірки вдвічі число інтервалів угруповання збільшується на 1. Зауважимо, що чим більше інтервалів угруповання, тим краще. Але, якщо брати число інтервалів, скажімо, порядку
, Тобто при збільшенні вибірки вдвічі число інтервалів угруповання збільшується на 1. Зауважимо, що чим більше інтервалів угруповання, тим краще. Але, якщо брати число інтервалів, скажімо, порядку  , То з ростом
, То з ростом  гістограма не наближатиметься до щільності.
гістограма не наближатиметься до щільності.
Справедливо наступне твердження:
Якщо щільність розподілу елементів вибірки є безперервною функцією, то при 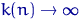 так що
так що 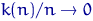 , Має місце поточкова збіжність за ймовірністю гістограми до щільності.
, Має місце поточкова збіжність за ймовірністю гістограми до щільності.
Так що вибір логарифма розумний, але не є єдино можливим.
висновок
Математична (або теоретична) статистика спирається на методи і поняття теорії ймовірностей, але вирішує в якомусь сенсі зворотні завдання.
Якщо ми спостерігаємо одночасно прояв двох (або більше) ознак, тобто маємо набір значень декількох випадкових величин - що можна сказати про їхню залежність? Є вона чи ні? А якщо є, то яка це залежність?
Часто буває можливо висловити деякі припущення про розподіл, захованому в «чорному ящику», або про його властивості. У цьому випадку за дослідними даними потрібно підтвердити або спростувати ці припущення ( «гіпотези»). При цьому треба пам'ятати, що відповідь «так» або «ні» може бути зроблено лише з певним ступенем достовірності, і чим довше ми можемо продовжувати експеримент, тим точніше можуть бути висновки. Найбільш сприятливою для дослідження виявляється ситуація, коли можна впевнено стверджувати про деякі властивості спостережуваного експерименту - наприклад, про наявність функціональної залежності між що спостерігаються величинами, про нормальність розподілу, про його симетричності, про наявність у розподілу щільності або про його дискретно характер, і т.д .
Отже, про (математичної) статистикою має сенс згадувати, якщо
· Є випадковий експеримент, властивості якого частково або повністю невідомі,
· Ми вміємо відтворювати цей експеримент в одних і тих же умовах деякий (а краще - яке завгодно) число раз.
Список літератури
1. Баумоль У. Економічна теорія і дослідження операцій. - М .; Наука, 1999..
2. Большев Л.Н., Смирнов Н.В. Таблиці математичної статистики. М .: Наука, 1995.
3. Боровков А.А. Математична статистика. М .: Наука, 1994.
4. Корн Г., Корн Т. Довідник з математики для науковців та інженерів. - СПБ: Видавництво «Лань», 2003.
5. Коршунов Д.А., Чернова Н.І. Збірник завдань і вправ з математичної статистики. Новосибірськ: Изд-во Інституту математики ім. С.Л.Соболева СО РАН, 2001..
6. Пехелецкій І.Д. Математика: підручник для студентів. - М .: Академия, 2003.
7. Суходольський В.Г. Лекції з вищої математики для гуманітаріїв. - СПБ Видавництво Санкт-Петербурзького державного університету. 2003
8. Феллер В. Введення в теорію ймовірностей та її застосування. - М .: Світ, Т.2, 1984.
9. Харман Г., Сучасний факторний аналіз. - М .: Статистика, 1972.
[1] Харман Г., Сучасний факторний аналіз. - М .: Статистика, 1972.
розділ: Математика
Кількість знаків з пробілами: 14862
Кількість таблиць: 5
Кількість зображень: 3
... Довести: За визначенням другої змішаної похідної. Знайдемо по двовимірної щільності одномірні щільності випадкових величин X і Y. Оскільки отримане рівність вірно для всіх х, то подинтегральную вираз аналогічно В математичної теорії ймовірності вводиться як базова формула (1) бо пропонується, що щільність ймовірності як аналітична функція може не існувати. Але тому що в нашому ...
... Для унімодальних симетричних розподілів майже 70% значень лежить в інтервалі. Властивості дисперсії: 1. Вплив на дисперсію збільшення кожного значення на якусь константу:, після виконання математичних операцій переконуємося, що дисперсія не змінюється. 2. Зміна дисперсії при множенні кожного вихідного значення на константу:, тобто дисперсія збільшується на квадрат константи. ...
... перевірити знання студента з першої частини курсу, яка викладається в перших чотирьох модулях. По-друге питаннях квитка перевіряються знання класичної граничної проблеми теорії ймовірностей і математичної статистики, які викладаються в наступних п'яти модулях. 1. Імовірнісна модель з не більше ніж рахунковим числом елементарних фіналів. Приклад: випробування з рівноможливими наслідками. 2. ...
... вибірок. 5. Дослідницькі проекти і їх захист. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Разом 10 5 10 Разом 60 34 Глава 2 Методика навчання школярів основам комбінаторики, теорії ймовірностей і математичної статистики в рамках профільної школи 2.1. Організація при формуванні просторового образу, c використанням ...
При цьому виникають, наприклад, такі питання: Якщо ми спостерігаємо одну випадкову величину - як по набору її значень в декількох дослідах зробити якомога точніший висновок про її розподілі?Що значить «по вибірці зробити висновок про розподіл»?
Ому?
Якщо ми спостерігаємо одночасно прояв двох (або більше) ознак, тобто маємо набір значень декількох випадкових величин - що можна сказати про їхню залежність?
Є вона чи ні?
А якщо є, то яка це залежність?