вибірковий метод

В и борочний м е тод, статистичний метод дослідження загальних властивостей сукупності будь-яких об'єктів на основі вивчення властивостей лише частини цих об'єктів, взятих на вибірку. Математична теорія В. м. Спирається на два важливих розділу математичної статистики - теорію вибору з кінцевої сукупності і теорію вибору з нескінченної сукупності. Основна відмінність В. м. Для кінцевої і нескінченної сукупностей полягає в тому, що в першому випадку В. м. Застосовується, як правило, до об'єктів невипадковою, детермінованою природи (наприклад, число дефектних виробів в даній партії готової продукції не є випадковою величиною : Це число - невідома постійна, яку і слід оцінити за вибірковими даними). У другому випадку В. м. Зазвичай застосовується для вивчення властивостей випадкових об'єктів (наприклад, для дослідження властивостей безперервно розподілених випадкових помилок вимірів, кожне з яких теоретично може бути витлумачено як реалізація одного з нескінченної кількості можливих результатів).

Вибір з кінцевої сукупності і його теорія є основою статистичних методів контролю якості і часто застосовуються в соціологічних дослідженнях (див. вибіркове спостереження ). Відповідно до теорії ймовірностей, вибірка буде правильно відображати властивості всієї сукупності, якщо вибір виробляється випадково, т. Е. Так, що будь-яка з можливих вибірок заданого обсягу n із сукупності обсягу N [число таких вибірок одно N! / N! (N - n) !] має однакову ймовірність бути фактично обраної.

На практиці найбільш часто використовується вибір без повернення (бесповторная вибірка), коли кожен відібраний об'єкт перед вибором наступного об'єкту в досліджувану сукупність; не повертається (такий вибір застосовується при статистичному контролі якості). Вибір з поверненням (вибірка з повторенням) розглядається зазвичай лише в теоретичних дослідженнях (прикладом вибору з поверненням є реєстрація числа часток, що торкнулися протягом даного часу стінок посудини, всередині якого відбувається броунівський рух ). Якщо n << N, то повторний і бесповторний вибори дають практично еквівалентні результати.

Властивості сукупності, досліджувані В. м., Можуть бути якісними і кількісними. У першому випадку завдання вибіркового обстеження полягає у визначенні кількості М об'єктів сукупності, що володіють якою-небудь ознакою (наприклад, при статистичному контролі часто цікавляться кількістю М дефектних виробів в партії обсягу N). Оцінкою для М служить відношення m N / n, де m - число об'єктів з даними ознакою в вибірці обсягу n. У разі кількісної ознаки мають справу з визначенням середнього значення сукупності 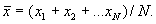оцінкою для 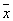є вибіркове середнє 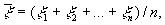де x 1, ..., xn - ті значення з досліджуваної сукупності x 1, x 2, ..., xN, які належать вибірці. З математичної точки зору 1-й випадок - приватна різновид 2-го, яка має місце, коли М величин x i дорівнюють 1, а решта (N - М) рівні 0; в цій ситуації 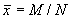і .

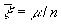У математичної теорії В. м. Оцінка середніх значень займає центральне місце тому, що до неї до певної міри зводиться вивчення мінливості ознаки усередині сукупності, так як за характеристику мінливості зазвичай приймають дисперсію

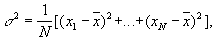
що представляє собою середнє значення квадратів відхилень xi від їх середнього значення 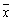. У разі вивчення якісної ознаки s 2 = М (N - M) / N 2.

Про точність оцінок m / n і 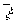судять по їх дисперсія

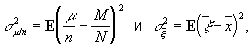
які в термінах дисперсії кінцевої сукупності s 2 виражаються у вигляді відносин s 2 / n (в разі вибірок з повторенням) і s 2 (N - n) / n (N - 1) (в разі бесповторном вибірок). Так як у багатьох практично цікавих завданнях випадкові величини m / n і 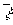при n ³ 30 приблизно підкоряються нормальному розподілу , То відхилення m / n від M / N і 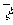від 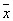, Що перевищують по абсолютній величині 2 sm / n і 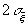відповідно, можуть при n ³ 30 здійснитися в середньому приблизно в одному випадку з двадцяти. Більш повну інформацію про розподіл кількісної ознаки в даній сукупності можна отримати за допомогою емпіричного розподілу цієї ознаки у вибірці.

Вибір з нескінченної сукупності. У математичній статистиці результати будь-яких однорідних спостережень (найчастіше незалежних) прийнято називати вибіркою навіть в тому випадку, коли ці результати не відповідають поняттю вибірки з повтореннями або без повторень з кінцевої сукупності. Наприклад, результати вимірювань кутів на місцевості, схильні до незалежним безперервно розподілених випадкових помилок, часто називають вибіркою з нескінченної сукупності. Передбачається, що принципово можна здійснити будь-яке число таких спостережень. Отримані фактично результати вважають вибіркою з нескінченної кількості можливих результатів, званих генеральною сукупністю.

Поняття генеральної сукупності не є логічно бездоганним і необхідним. Для вирішення практичних завдань потрібна не сама нескінченна генеральна сукупність, а лише ті чи інші характеристики, які їй ставляться у відповідність. Ці характеристики з точки зору теорії ймовірностей є числовими або функціональними характеристиками деякого розподілу ймовірностей, а елементи вибірки -Випадкові величинами, котрі підпорядковуються цим розподілом. Таке тлумачення дозволяє розповсюдити на вибіркові оцінки загальну теорію статистичних оцінок .

З цієї причини, наприклад, в ймовірнісної теорії обробки спостережень поняття нескінченної генеральної сукупності замінюється поняттям розподілу ймовірностей, що містить невідомі параметри. Результати спостережень тлумачаться як експериментально спостережувані значення випадкових величин, що підкоряються цим розподілом, Мета обробки - обчислення за результатами спостережень в тому чи іншому сенсі оптимальних статистичних оцінок для невідомих параметрів розподілу.

Літ .: Дунін-Барковський І. В., Смирнов Н. В., Теорія ймовірностей і математична статистика в техніці (Загальна частина), М., 1955, гл. 5; Кендалл М., Стьюарт А., Теорія розподілів, пров. з англ., М., 1966.

Л. Н. Большев.