Підгонка параметрів різних моделей гіперпружних матеріалів для відповідності експериментальним даним

1. Метод підгонки в середовищі COMSOL Multiphysics
2. Ізотропна, майже нестисливої ​​гіперпружних середовище (гіперпружних)
3. Залежність напруги від головних значень розтягування в моделях нестискуваних гіперпружних матеріалів
4. Модель Нео-Хукена (Neo-Hookean)
5. Модель Муні-Рівлін (Mooney-Rivlin) з двома параметрами
6. Модель Муні-Рівлін, п'ять параметрів
7. Модель Арруда-Бойса (Arruda-Boyce)
8. Модель Йо (Yeoh)
9. Модель Огдена (Ogden)
10. Чисельна підгонка в програмному середовищі COMSOL Multiphysics за допомогою інтерфейсу Оптимізації
11. ЗАКЛЮЧНІ зауваження

Раніше в блозі ми обговорили необхідність отримання спеціальним чином виміряних даних, щоб підігнати параметри відповідної моделі середовища. Ми розглянули також типові експериментальні методи і умови їх проведення, які необхідно враховувати при виборі моделі середовища, і навели приклад використання результатів вимірювання безпосередньо в моделі нелінійної пружної середовища. Сьогодні ми сконцентруємося на тому, як підібрати параметри в різних моделях гіперпружних матеріалів таким чином, щоб найкращим чином описати отримані експериментальні дані.

Метод підгонки в середовищі COMSOL Multiphysics

Наступним питанням, після отримання результатів вимірювання є: яким чином з них можна отримати параметри, необхідні (необхідні) для опису моделі гіперпружних середовища? Один з можливих способів, використовуваних в середовищі COMSOL Multiphysics - це підгонка параметризрвані аналітичної функції до експериментально виміряним результатам за допомогою Модуля Оптимізації.

У наступному розділі, ми визначимо аналітичні вирази, що зв'язують тензори напружень і деформації, для двох зазвичай проводяться тестів - одноосного і рівномірного двуосного - розтягування уздовж однієї осі і рівномірного розтягування по двох осях одночасно. Потім ми використовуємо ці аналітичні вирази для підгонки до результатів вимірювань з метою отримання параметрів середовища.

Ізотропна, майже нестисливої ​​гіперпружних середовище (гіперпружних)

Точний опис об'ємної деформації гіперпружних матеріалів для оцінки матеріальних параметрів середовища є дуже громіздкою процедурою. Найчастіше замість цього, передбачається повна нестисливі середовища і виконується оцінка корисних властивостей за допомогою підгонки. Після цієї оцінки підбирається правдоподібне значення модуля об'ємного стиснення майже нестисливого гіперпружних матеріалу, так як це значення не вирахував.

У цій статті, виміряні дані будуть використовуватися для підгонки параметрів декількох моделей повністю нестискуваних гіперпружних матеріалів. Почнемо з огляду деяких базових концепцій, що лежать в основі поняття майже нестисливої ​​середовища, а потім охарактеризуємо процес вимірювання тиску для випадку повної несжимаемости.

Для майже нестисливої ​​гіперпружних середовища, повна щільність енергії деформації представляється у вигляді

W_s = W_ {iso} + W_ {vol}

де W_ {iso} і W_ {vol} - ізохорно і об'ємна щільності енергії деформації, відповідно. Другий тензор напружень Піола-Кірхгофа визначається виразом

S = -p_pJC ^ {- 1} +2 \ frac {\ partial W_ {iso}} {\ partial C}

де p_ {p} - об'ємне напруга, J - відносна зміна обсягу, і C - правий тензор Коші-Гріна.

Розкладемо другий член цього рівняння, так що другий тензор напруги Піола-Кірхгофа буде дорівнює

S = -p_pJC ^ {- 1} +2 \ left (J ^ {- 2/3} \ left (\ frac {\ partial W_ {iso}} {\ partial \ bar {I_ {1}}} + \ bar {I_ {1}} \ frac {\ partial W_ {iso}} {\ partial \ bar {I_ {2}}} \ right) IJ ^ {- 4/3} \ frac {\ partial W_ {iso}} { \ partial \ bar {I} _ {2}} C - \ left (\ frac {\ bar {I_ {1}}} {3} \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {1}} + \ frac {2 \ bar {I} _ {2}} {3} \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {2}} \ right) C ^ {- 1} \ right)

де \ bar {I} _ {1} і \ bar {I} _ {2} - інваріанти ізохоричного правого тензора Коші-Гріна \ bar {C} = J ^ {- 2/3} C

Перший тензор напружень Піоли-Кірхгофа, P, і тензор напружень Коші, \ sigma, можуть бути виражені через другий тензор напружень Піоли-Кірхгофа за допомогою операцій

\ Begin {align} P & = FS \\
\ Sigma & = J ^ {- 1} FSF ^ {T}
\ End {align}

Тут F - градієнт деформації.

Зауваження: Більш докладний опис вимірювань різних напруг можна знайти в попередній статті нашого блогу " Why All These Stresses and Strains? "

Щільність енергії деформації та напруги часто виражаються в залежності від ступеня розтягування \ lambda. Ступінь розтягування є мірою деформації. При розтягуванні уздовж однієї осі (одноосний експеримент) ступінь розтягування (надалі просто розтягнення) визначається як \ lambda = L / L_0, де L - довжина зразка в деформованому стані і L_0 - його первісна довжина. У багатовісним напруженому стані можна обчислити головні значення розтягувань \ lambda_a \; (a = 1,2,3) уздовж головних напрямків \ hat {\ mathbf {N} _a}, які збігаються з напрямками головних напружень. Компоненти тензора напружень можуть бути записані в спектральної формі як

S = \ sideset {} {^ 3_ {a = 1}}
\ Sum S_ {a} \ hat {\ mathbf {N} _ {a}} \ otimes \ hat {\ mathbf {N} _ {a}}

де S_ {a} представляє головні значення другого тензора напружень Піоли-Кирхгофа і \ hat {\ mathbf {N} _ {a}} представляє головні виділені напрямки. Ми можемо також уявити правий тензор Коші-Гріна в його спектральної формі як

C = \ sideset {} {^ 3_ {a = 1}}
\ Sum \ lambda_a ^ 2 \ hat {\ mathbf {N} _a} \ otimes \ hat {\ mathbf {N} _a}

де \ lambda_a позначає головні значення розтягувань. Це дозволяє висловити головні значення другого тензора напружень Піоли-Кирхгофа через головні значення розтягувань (у вигляді функції від головних значень розтягнень)

S_a = \ frac {-p_p J} {\ lambda_a ^ 2} +2 \ left (J ^ {- 2/3} \ left (\ frac {\ partial W_ {iso}} {\ partial \ bar {I_ {1 }}} + \ bar {I_ {1}} \ frac {\ partial W_ {iso}} {\ partial \ bar {I_ {2}}} \ right) -J ^ {- 4/3} \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {2}} \ lambda_a ^ 2 - \ frac {1} {\ lambda_a ^ 2} \ left (\ frac {\ bar {I_ {1}}} {3} \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {1}} + \ frac {2 \ bar {I} _ {2}} {3} \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {2}} \ right) \ right)

Розглянемо тепер експерименти одно- і двухосного розтягування / стиснення, описані в першій статті нашого блогу із серії «Конструкційні Матеріали». Для обох цих матеріальних тестів можна отримати загальне співвідношення між напругою і розтягуванням.

У припущенні несжимаемости (J = 1) головні розтягування для одноосной деформації изотропного гіперпружних матеріалу визначаються значеннями

\ Lambda_1 = \ lambda, \ lambda_2 = \ lambda_3 = \ lambda ^ {- 1/2}

Градієнт деформації запишеться у вигляді

\ Begin {array} {c} F = \\ \ end {array} \ left (\ begin {array} {ccc} \ lambda & 0 & 0 \\ 0 & \ frac {1} {\ sqrt {\ lambda}} & 0 \\ 0 & 0 & \ frac {1} {\ sqrt {\ lambda}} \ end {array} \ right)

Для одноосного розтягу S_2 = S_3 = 0 об'ємне напруга p_ {p} можна виключити, тоді

(1)

S_ {1} = 2 \ left (\ frac {1} {\ lambda} - \ frac {1} {\ lambda ^ 4} \ right) \ left (\ lambda \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {1_ {uni}}} + \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {2_ {uni}}} \ right), \; P_1 = \ lambda S_1 \; \ Sigma_1 = \ lambda ^ 2 S_1, \; \; \; \;

Ізохорно інваріанти \ bar {I} _ {1_ {uni}} і \ bar {I} _ {2_ {uni}} можуть бути виражені через головне розтягнення \ lambda як

\ Begin {align *}
\ Bar {I} _ {1_ {uni}} = \ left (\ lambda ^ 2 + \ frac {2} {\ lambda} \ right) \\
\ Bar {I} _ {2_ {uni}} = \ left (2 \ lambda + \ frac {1} {\ lambda ^ 2} \ right)
\ End {align *}

У припущенні несжимаемости головні значення розтягнень для рівномірної двухосной деформації изотропного гіперпружних матеріалу визначаються співвідношеннями

\ Lambda_1 = \ lambda_2 = \ lambda, \; \ Lambda_3 = \ lambda ^ {- 2}

Для рівномірного двухосного розтягування S_3 = 0 об'ємне напруга p_ {p} можна виключити, тоді

(2)

S_1 = S_2 = 2 \ left (1 \ frac {1} {\ lambda ^ 6} \ right) \ left (\ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {1_ {bi }}} + \ lambda ^ 2 \ frac {\ partial W_ {iso}} {\ partial \ bar {I} _ {2_ {bi}}} \ right), \; P_1 = \ lambda S_1, \; \ Sigma_1 = \ lambda ^ 2 S_1 \; \; \; \;

Інваріанти \ bar {I} _ {1_ {bi}} і \ bar {I} _ {2_ {bi}} тоді даються виразами

\ Begin {align *}
\ Bar {I} _ {1_ {bi}} = \ left (2 \ lambda ^ 2 + \ frac {1} {\ lambda ^ 4} \ right) \\
\ Bar {I} _ {2_ {bi}} = \ left (\ lambda ^ 4 + \ frac {2} {\ lambda ^ 2} \ right)
\ End {align *}

Залежність напруги від головних значень розтягування в моделях нестискуваних гіперпружних матеріалів

Розглянемо співвідношення між напругою і розтягуванням для декількох найбільш поширених моделей гіперпружних матеріалів. Для підгонки параметрів моделей буде застосовуватися перший тензор напружень Піоли-Кірхгофа.

Модель Нео-Хукена (Neo-Hookean)

Повна щільність енергії деформації в моделі середовища Нео-Хукена дається виразом

W_s = \ frac {1} {2} \ mu \ left (\ bar {I} _1-3 \ right) + \ frac {1} {2} \ kappa \ left (J_ {el} -1 \ right) ^ 2

де J_ {el} - відносна зміна пружного обсягу, \ mu - матеріальний параметр, який потрібно обчислити за допомогою чисельної підгонки. За умови повної несжимаемости, використовуючи рівняння (1) і (2) , Вираження першого напруги Піоли-Кирхгофа для випадків одноосной і рівномірної двухосной деформації перетворюються до вигляду

\ Begin {align *}

P_ {1_ {uniaxial}} & = \ mu \ left (\ lambda- \ lambda ^ {- 2} \ right) \\
P_ {1_ {biaxial}} & = \ mu \ left (\ lambda- \ lambda ^ {- 5} \ right)
\ End {align *}

Залежність напруги від розтягування для деяких інших моделей гіперпружних матеріалів наводяться нижче. Вони легко можуть бути отримані за допомогою рівнянь (1) і (2) , Які пов'язують напруга і щільність енергії деформації.

Модель Муні-Рівлін (Mooney-Rivlin) з двома параметрами

\ Begin {align *}
P_ {1_ {uniaxial}} & = 2 \ left (1 \ lambda ^ {- 3} \ right) \ left (\ lambda C_ {10} + C_ {01} \ right) \\
P_ {1_ {biaxial}} & = 2 \ left (\ lambda- \ lambda ^ {- 5} \ right) \ left (C_ {10} + \ lambda ^ 2 C_ {01} \ right)
\ End {align *}

Тут C_ {10} і C_ {01} - матеріальні параметри Муні-Рівлін.

Модель Муні-Рівлін, п'ять параметрів

\ Begin {align} \ begin {split}
P_ {1_ {uniaxial}} & = 2 \ left (1 \ lambda ^ {- 3} \ right) \ left (\ lambda C_ {10} + 2C_ {20} \ lambda \ left (I_ {1_ {uni} } -3 \ right) + C_ {11} \ lambda \ left (I_ {2_ {uni}} - 3 \ right) \\
& \ Quad + C_ {01} + 2C_ {02} \ left (I_ {2_ {uni}} - 3 \ right) + C_ {11} \ left (I_ {1_ {uni}} - 3 \ right)) \ right) \\
P_ {1_ {biaxial}} & = 2 \ left (\ lambda- \ lambda ^ {- 5} \ right) \ left (C_ {10} + 2C_ {20} \ left (I_ {1_ {bi}} - 3 \ right) + C_ {11} \ left (I_ {2_ {bi}} - 3 \ right) \\
& \ Quad + \ lambda ^ 2C_ {01} +2 \ lambda ^ 2C_ {02} \ left (I_ {2_ {bi}} - 3 \ right) + \ lambda ^ 2 C_ {11} \ left (I_ {1_ {bi}} - 3 \ right)) \ right)
\ End {split}
\ End {align}

Тут C_ {10}, C_ {01}, C_ {20}, C_ {02}, і C_ {11} - матеріальні параметри Муні-Рівлін.

Модель Арруда-Бойса (Arruda-Boyce)

\ Begin {align}
P_ {1_ {uniaxial}} & = 2 \ left (\ lambda- \ lambda ^ {- 2} \ right) \ mu_0 \ sum_ {p = 1} ^ {5} \ frac {p c_p} {N ^ {p -1}} I_ {1_ {uni}} ^ {p-1} \\
P_ {1_ {biaxial}} & = 2 \ left (\ lambda- \ lambda ^ {- 5} \ right) \ mu_0 \ sum_ {p = 1} ^ {5} \ frac {p c_p} {N ^ {p -1}} I_ {1_ {bi}} ^ {p-1}
\ End {align}

Тут \ mu_0 і N - матеріальні параметри Арруда-Бойса, і c_p - п'ять перших членів розкладання в ряд Тейлора зворотної функції Ланжевена.

Модель Йо (Yeoh)

\ Begin {align}
P_ {1_ {uniaxial}} & = 2 \ left (\ lambda- \ lambda ^ {- 2} \ right) \ sum_ {p = 1} ^ {3} p c_p \ left (I_ {1_ {uni}} - 3 \ right) ^ {p-1} \\
P_ {1_ {biaxial}} & = 2 \ left (\ lambda- \ lambda ^ {- 5} \ right) \ sum_ {p = 1} ^ {3} p c_p \ left (I_ {1_ {bi}} - 3 \ right) ^ {p-1}
\ End {align}

Тут значення c_p - матеріальні параметри Yeoh.

Модель Огдена (Ogden)

\ Begin {align}
P_ {1_ {uniaxial}} & = \ sum_ {p = 1} ^ {N} \ mu_p \ left (\ lambda ^ {\ alpha_p-1} - \ lambda ^ {- \ frac {\ alpha_p} {2} - 1} \ right) \\
P_ {1_ {biaxial}} & = \ sum_ {p = 1} ^ {N} \ mu_p \ left (\ lambda ^ {\ alpha_p-1} - \ lambda ^ {- 2 \ alpha_p-1} \ right)
\ End {align}

Тут \ mu_p і \ alpha_p - матеріальні параметри Огдена.

Чисельна підгонка в програмному середовищі COMSOL Multiphysics за допомогою інтерфейсу Оптимізації

Використовуючи інтерфейс Оптимізації в середовищі COMSOL Multiphysics, ми будемо підганяти теоретичну криву, яка розраховується за допомогою аналітичних виразів, детально описаних вище, до експериментально виміряної залежності напруги від розтягування. Відзначимо, що використовуються тут експериментальні дані - це номінальна напруга, яке визначається як сила в поточній конфігурації, діюча на первісну (недеформованому) площа зразка. Дуже важливо, щоб чисельні і виміряні дані, які використовуються в підгонці, відповідали один одному. Отже, для підгонки до виміряних даними будуть застосовуватися аналітичні вирази для першого тензора напружень Піоли-Кірхгофа. Графік нижче показує виміряні значення номінального напруги (необроблені дані) при одноосьовому і рівномірному двухосном розтягуванні вулканізованої гуми.

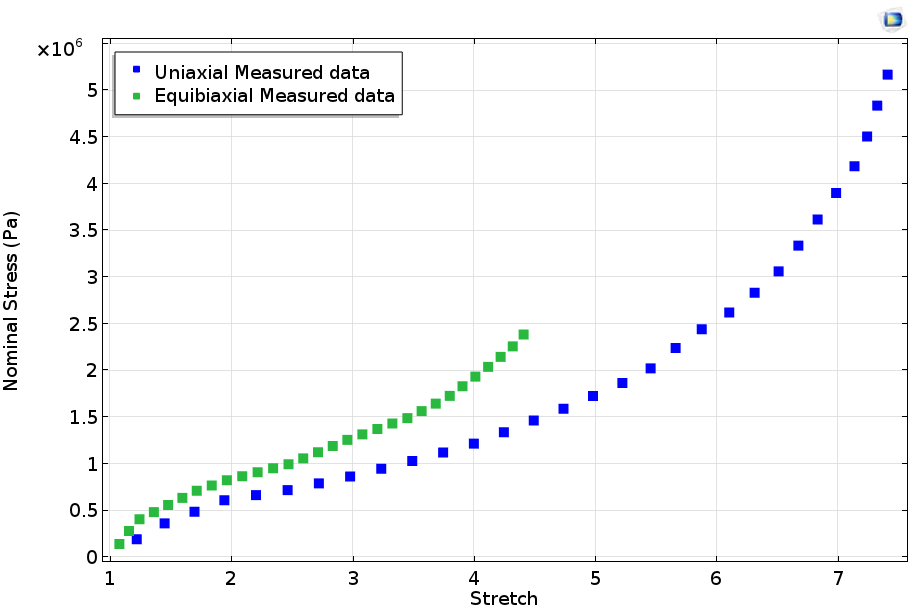
Виміряна залежність напруга-деформація, зі статті Treloar .

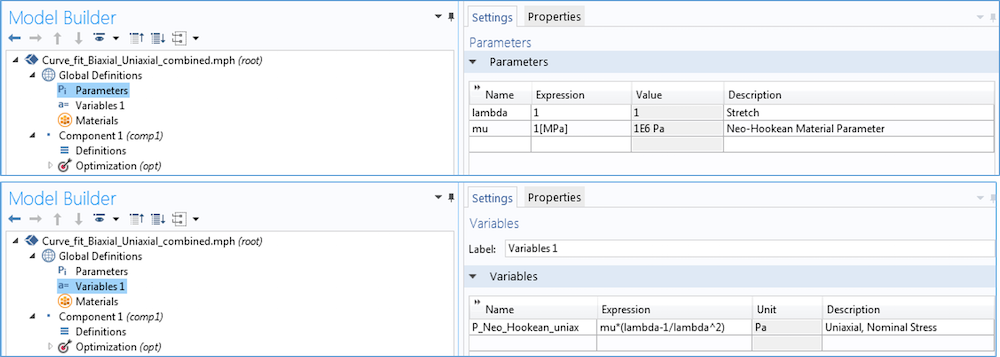
Почнемо з настройки моделі Нео-Хукена для підгонки результатів одноосного експерименту. Першим кроком є додавання інтерфейсу Оптимізація до 0D моделі. Тут 0D на увазі, що наш аналіз не прив'язаний до конкретної геометрії.

Потім можна визначити матеріальні параметри, які необхідно обчислити, і змінні для аналітичної залежності напруги від розтягування. На зображенні нижче показаний вибір параметрів і змінної, що визначаються для випадку одноосного розтягу в матеріальної моделі Нео-Хукена.

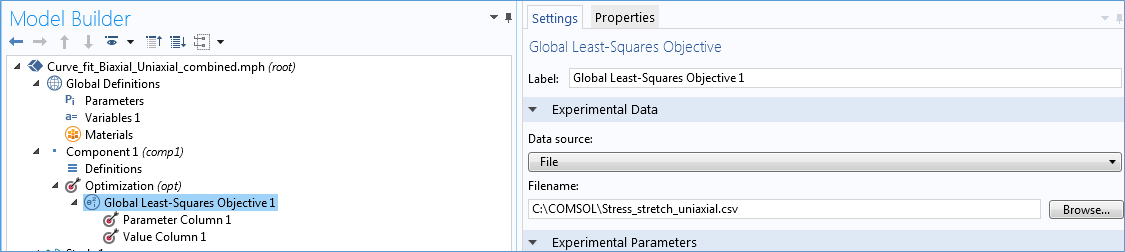
Усередині інтерфейсу Оптимізація, є розділ Глобальний об'єкт методу найменших квадратів (Global Least-Squares Objective), в якому можна вказати вхідний файл з виміряної в одноосьовому експерименті залежністю напруга-деформація. Далі є пункти Стовпець параметрів (Parameter Column) і Стовпець значень (Value Column). Тут в якості вимірюваного параметра задається лямбда (розтягнення) і вказується аналітичний вираз залежності напруга -деформація для одноосного розтягу, яке буде використовуватися для підгонки до виміряних даними. Можна також вказати ваговій множник в пункті Стовпець вагових коефіцієнтів (Column contribution weight). Більш детальна інформація про параметри поділу Глобальний об'єкт методу найменших квадратів (Global Least-Squares Objective) доступна в навчальному додатку Чисельна підгонка моделі Муні-Рівлін (Mooney-Rivlin Curve Fit tutorial) , Розташованому в нашій Галереї додатків.

Тепер ми готові до того, щоб вирішити вищезгадану задачу, а саме, оцінити матеріальні параметри за допомогою підгонки результатів експерименту по одноосьовому розтягування в рамках моделі Нео-Хукена. Однак навряд чи це буде гарною ідеєю. В першій частині блог-серії пояснюється, що цей, здавалося б, простий тест має занадто багато неврахованих чинників параметрів. Нижче ми продемонструємо наслідки калібрування матеріалу, засновані тільки на одному наборі вхідних даних.

Залежно від умов експерименту кращу оцінку матеріальних параметрів можна отримати, використовуючи комбінації різних вимірювальних методів: одновісне розтягнення / стиснення, двовісне розтягнення, кручення і т.д. Зібрані таким чином дані можна використовувати для підгонки, представивши напруга в аналітичному вигляді в кожному з розглянутих випадків.

У цій статті спільно використовуються результати експериментів по одноосьовому і рівномірному двовісний розтягування досліджуваного зразка. Точно так же, як ми налаштовували модель оптимізації для одноосного тесту, визначимо іншу процедуру глобальної мінімізації для рівномірного двухосного тесту, а також супутні їй параметри і значення. У другій процедурі глобальної мінімізації вкажемо в якості вхідних даних файл з результатами вимірювань напруга-деформація двухосного експерименту. У стовпці значень виберемо аналітичний вираз для напруги в двухосном експерименті, яке буде використовуватися для підгонки по виміряним даними.

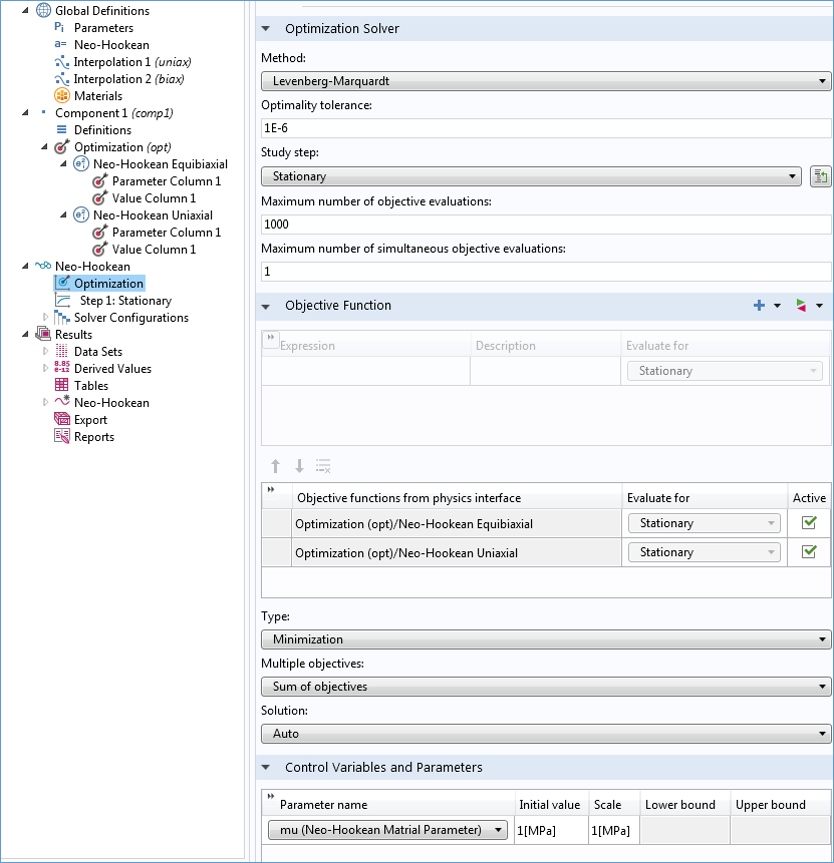
Налаштування для кроку Оптимізації наведені на зображенні нижче. Розділи в деревовидному каталозі перейменовані вручну, щоб відобразити використовувану модель (Нео-Хукен) і два набори експериментальних даних (одноосний і рівномірний двовісний тести). Алгоритмом оптимізації є метод Левенберга-Марквардта (Levenberg-Marquardt), який використовується для вирішення завдань методом найменших квадратів. Тепер модель налаштована таким чином, щоб оптимізувати пошук глобального мінімуму за двома розділами даних - одноосного і двухосного експериментів.

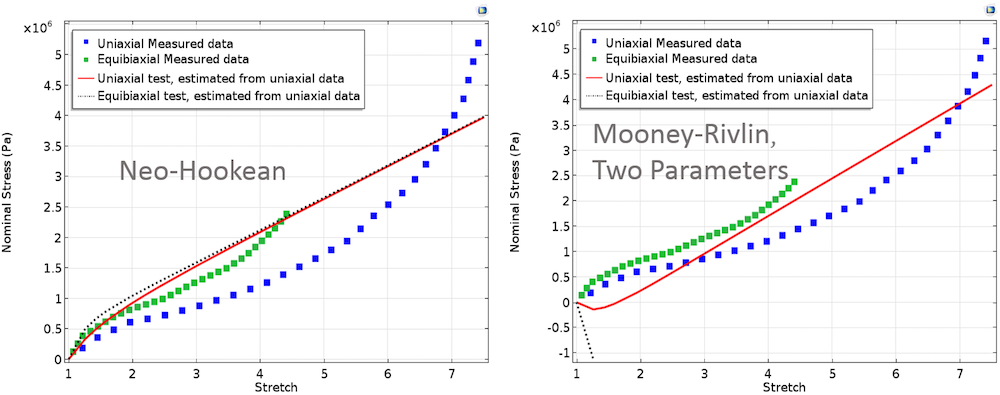
Графік нижче представляє результат порівняння змодельованих і виміряних даних. Рівні вагові множники присвоювалися обом наборам експериментальних даних (одноосьовому і двовісний) для підгонки методом найменших квадратів. Очевидно, що модель Нео-Хукена з усього лише одним регульованим параметром не може забезпечити належного відповідності з експериментальними даними, які є нелінійними і мають одну точку перегину.

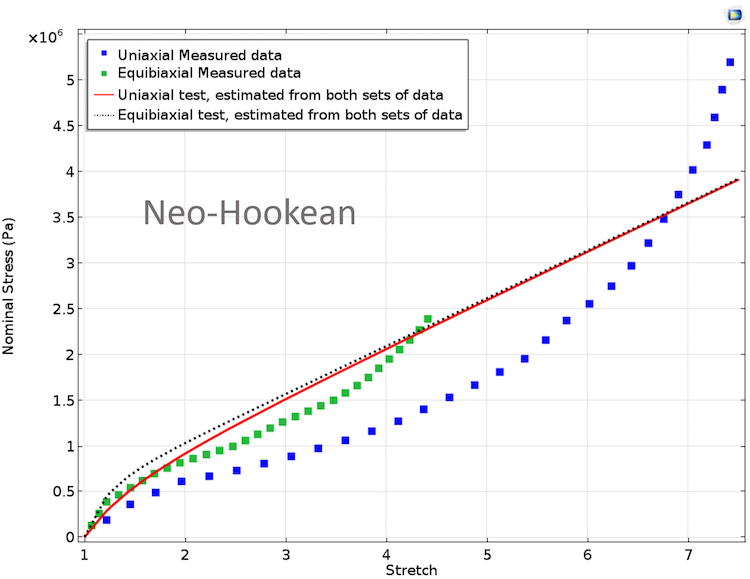
Підгонка матеріальних параметрів в моделі Нео-Хукена. Рівні вагові множники присвоювалися обом наборам експериментальних даних.

Підгонка кривих з нерівними ваговими множниками для двох тестових наборів даних призведе до незначної зміни підганяються кривих. Подібно моделі Нео-Хукена налаштуємо процедуру оптимізації за методом найменших квадратів, відповідну моделям гіперпружних матеріалів Муні-Рівлін, Арруда-Бойса, Йо і Огдена. В обчисленнях, представлених нижче, ми включимо в розгляд обидва випадки рівних і нерівних вагових множників.

У разі неоднакових ваг, більший, але довільним чином обраний множник буде використовуватися для повного набору даних двухосного експерименту. Принципово можна привласнити нерівні ваги тільки для деякого діапазону значень відносних розтягувань замість повного набору даних. У цьому окремому випадку потрібно розділити вхідні дані на частини, використовуючи окремі розділи Глобальний об'єкт методу найменших квадратів (Global Least-Squares Objective) для кожного діапазону значень розтягування. Це дозволить коректувати вагові множники в різних діапазонах значень розтягування.

Перелічені нижче графіки представляють криві підгонки для різних матеріальних моделей з рівними і нерівними ваговими множниками і відповідають двом тестовим експериментів.

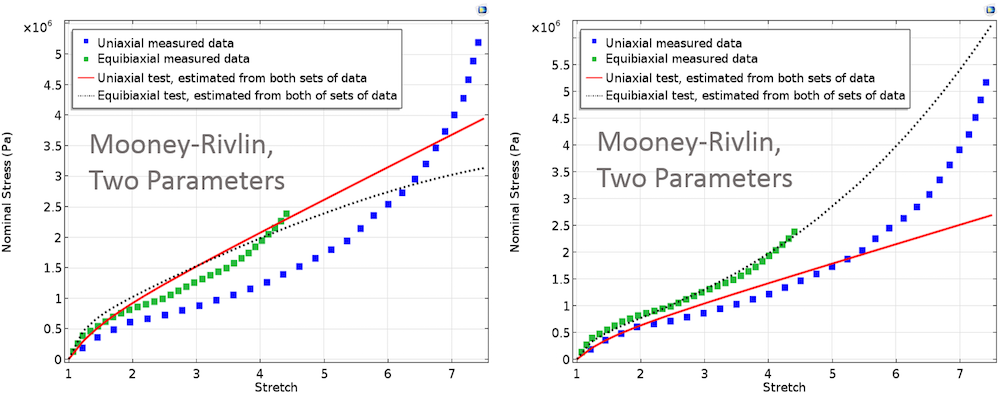
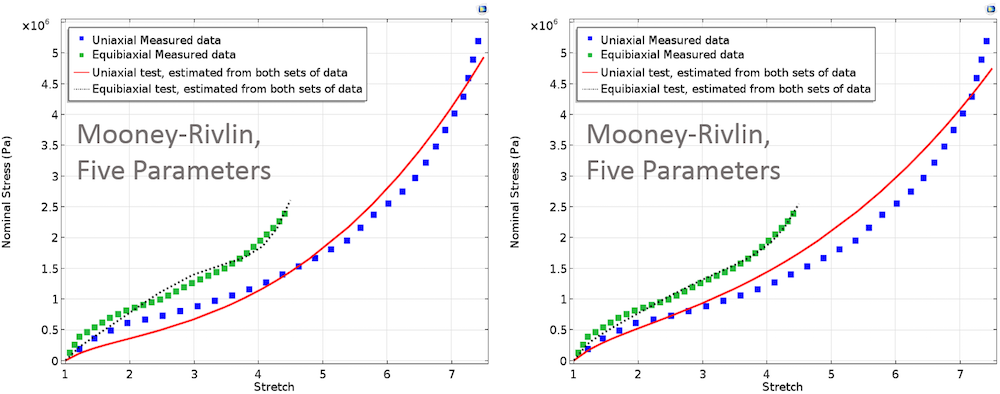
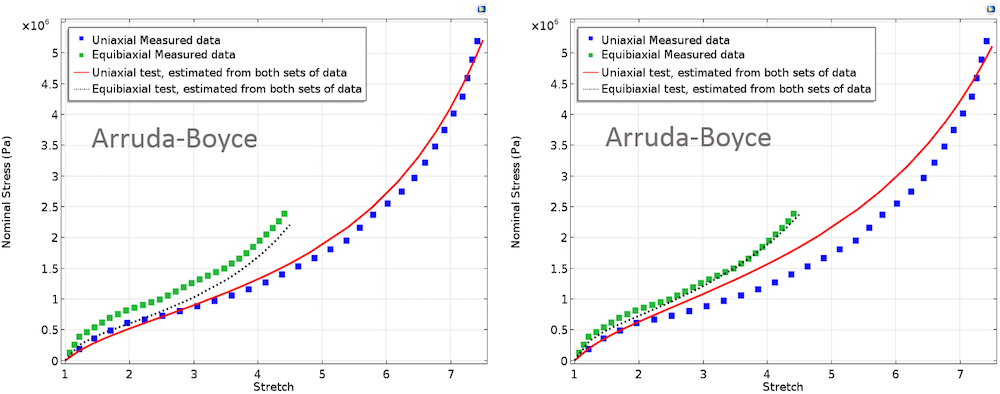
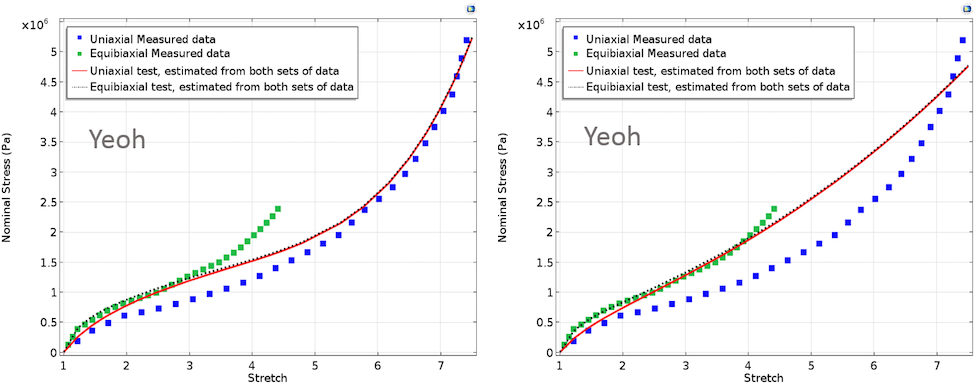
Зліва: Криві підгонки, отримані в рамках моделей Муні-Рівлін, Арруда-Бойса і Йо. В цьому випадку, однакові вагові множники присвоювалися обом наборам експериментальних даних. Справа: Криві підгонки, отримані в рамках моделей Муні-Рівлін, Арруда-Бойса і Йо. Тут, більш високий вагу присвоювався даними двухосного експерименту.

Модель Огдена з трьома складовими дуже добре описує обидва набору експериментальних даних в разі, коли їм присвоєні рівні вагові множники.

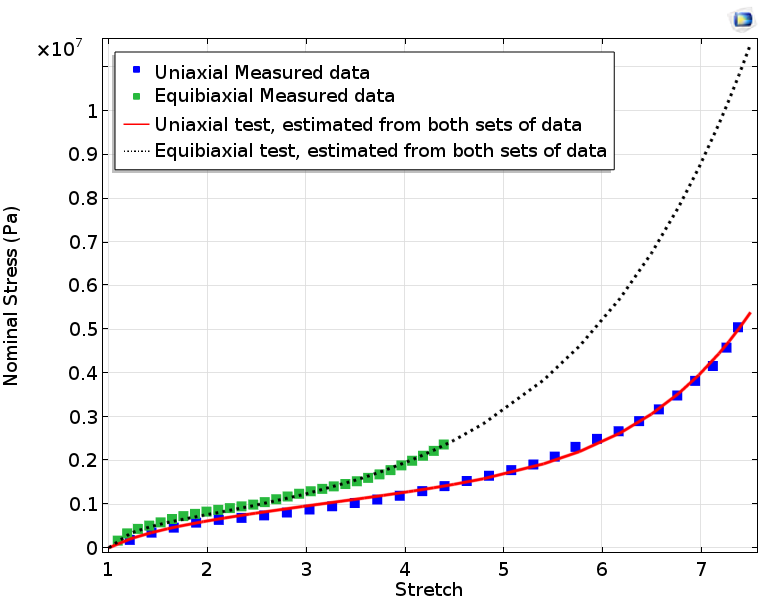
Криві підгонки, отримані в рамках моделі Огдена з трьома складовими.

У разі, коли підгонка здійснюється тільки з одноосьовим набором даних, а потім обчислені значення параметрів використовуються в розрахунку графічної залежності для двовісного експерименту, ми отримаємо результати, графічно представлені нижче. Ці графіки демонструють повну невідповідність розрахункових і виміряних залежностей для рівномірного двухосного розтягування зразка. При оцінці матеріальних параметрів найкраще виконувати підгонку з комбінованим набором даних, отриманих в різних режимах деформації, і уникати використання даних тільки однієї деформационной моди.

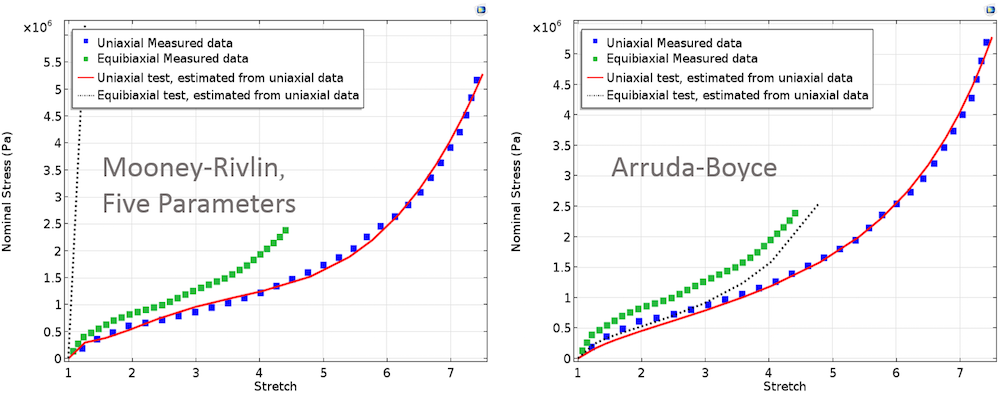
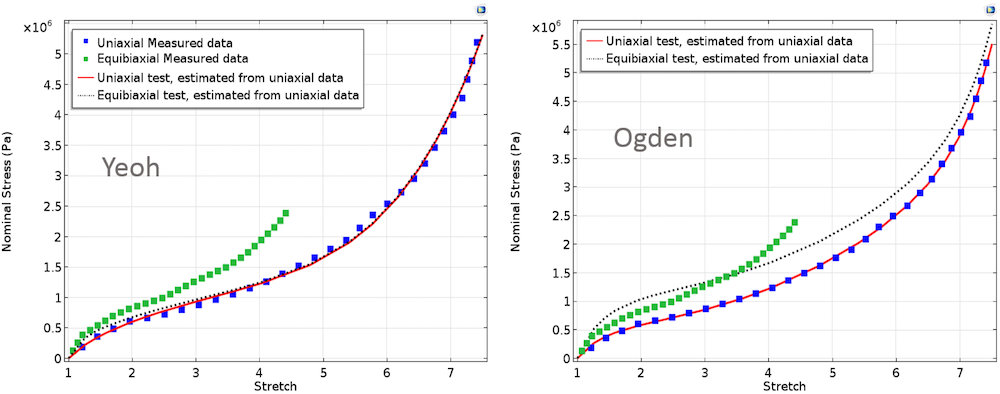
Одновісне і двовісне напруги, обчислені підгонкою модельних параметрів з використанням даних тільки одноосного експерименту.

ЗАКЛЮЧНІ зауваження

Визначення матеріальніх параметрів для моделей гіперпружніх середовище с помощью підгонкі аналітичних кривих может здати надійнім методом. Однако патенти, такоже враховуваті устоячівость даної моделі гіперпружніх матеріалу. Критерій для визначення стійкості відомий як стійкість по Друкеру (Drucker stability) . Згідно з критерієм Друкера, приріст роботи, викликане відповідним збільшенням напруги, завжди має бути більше нуля. Якщо критерій порушується, модель матеріалу буде нестійкою.

У цій блог-статті ми продемонстрували, як можна використовувати інтерфейс Оптимізації (Optimization) в середовищі COMSOL Multiphysics для підгонки аналітичних кривих до множинного набору експериментальних даних. Альтернативний спосіб підгонки, який не вимагає інтерфейсу Оптимізації також був темою обговорення в більш ранній блог-статті . Аналогічно тому, як ми використовували тут дані одноосного і двухосного розтягування зразка для оцінки матеріальних параметрів, можна виконувати підгонку експериментальних даних, отриманих за допомогою зсувних і об'ємних тестів, для характеристики інших станів деформації.

Для більш докладних покрокових інструкцій про те, як використовувати інтерфейс Оптимізації для підгонки кривих, ознайомтеся з навчальним додатком Чисельна підгонка моделі Муні-Рівлін (Mooney-Rivlin Curve Fit tutorial) в нашій Галереї додатків.