Регресія (математіч.)

Реграм е ссія в теорії ймовірностей і математичній статистиці, залежність середнього значення якої-небудь величини від деякої іншої величини або від декількох величин. На відміну від чисто функціональної залежності у = f (х), коли кожному значенню незалежної змінної х відповідає одне певне значення величини у, при регресійної зв'язку одному і тому ж значенню х можуть відповідати залежно від випадку різні значення величини у. Якщо при кожному значенні х = xi спостерігається ni, значень yi 1, ..., 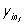величини у, то залежність середніх арифметичних 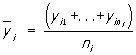від xi і є Р. в статистичному розумінні цього терміна. Прикладом такого роду залежності служить, зокрема, залежність середніх діаметрів сосен від їх висот; см. табл. в ст. кореляція .

Вивчення Р. в теорії вірогідності засноване на тому, що випадкові величини Х і Y, які мають спільний розподіл вірогідності, пов'язані ймовірнісної залежністю: при кожному фіксованому значенні Х = х величина Y є випадковою величиною з певним (залежним від значення х) умовним розподілом ймовірностей. Р. величини Y по величині Х визначається умовним математичним очікуванням Y, обчисленим за умови, що Х = х:

Е (Y ê х) = u (х).

Рівняння у = u (х), в якому х грає роль «незалежної» змінної, називається рівнянням регресії, а відповідний графік - лінією регресії величини Y по X. Точність, з якою рівняння Р. Y по Х відображає зміну Y в середньому при зміні х, вимірюється умовною дисперсією величини Y, обчисленою для кожного значення х = х:

D (Y ê х) = s2 (x).

Якщо s 2 (х) = 0 при всіх значеннях х, то можна з достовірністю стверджувати, що Y і Х пов'язані суворої функціональної залежністю Y = u (X). Якщо s 2 (х) = 0 при всіх значеннях х і u (х) не залежить від х, то кажуть, що Р. Y по Х відсутній. Аналогічним чином визначається Р. Х по Y і зокрема, рівняння Р. х = u (у), = Е (Х ï Y = у). Функції у = u (х) і х = u (у), взагалі кажучи, не є взаємно зворотними.

Лінії Р. володіють наступною чудовою властивістю: серед всіх дійсних функцій f (х) мінімум математичного очікування Е [Y - f (X)] 2 досягається для функції f (x) = u (х), т. Е. Р. Y по Х дає найкраще, у вказаному сенсі, уявлення величини Y по величині X. Ця властивість використовується для прогнозу Y по X: якщо значення Y безпосередньо не спостерігається і експеримент дозволяє реєструвати лише компоненту Х вектора (X, Y), то в якості прогнозованого значення Y використовують величину u (X).

Найбільш простим є випадок, коли Р. Y по Х лінійна:

Е (Y ï x) = b 0 + b 1 x.

Коефіцієнти b 0 і b 1, називаються коефіцієнтами регресії, визначаються рівністю

,

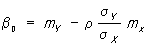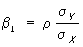
де m Х і m Y - математичні очікування Х і Y, 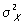і 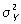- дисперсії Х і Y, а r - коефіцієнт кореляції між Х і Y. Рівняння Р. при цьому виражається формулою

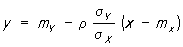
У разі, коли спільний розподіл Х і Y нормально, обидві лінії Р. в = u (х) і х = u (у) є прямими.

Якщо Р. Y по Х відмінна від лінійної, то останнє рівняння є лінійна апроксимація дійсного рівняння Р .: математичне чекання Е [Y - b 0 - b 1 X] 2достігает мінімуму b 0 і b 1 при b 0 = b0 і b 1 = b 1. Особливо часто зустрічається випадок рівняння Р., що виражається лінійною комбінацією тих або інших заданих функцій:

у = u (Х) = b 0 j0 (x) + b 1 j1 (x) + ... + bm jm (x).

Найбільш важливе значення має параболічна (поліноміальна) Р., при якій j 0 (x) = 1, j 1 (x) = x, ..., jm (x) = x m.

Поняття Р. застосовне не тільки до випадкових величин, але і до випадкових векторів. Зокрема, якщо Y - випадкова величина, а Х = (X1, ..., Xk) - випадковий вектор, що мають спільний розподіл вірогідності, то Р. Y по X визначається рівнянням

y = u (x 1, ..., x k),

де u (x 1, ..., x k) = E {Y ï X = x 1, ..., X k = x k}.

якщо

u (x 1, ..., x k) = b 0 + b 1 x 1 + ... + bk x k,

то Р. називається лінійної. Ця форма рівняння Р. включає в себе багато типів Р. з однією незалежною змінною, зокрема поліноміальна Р. Y по Х порядку k зводиться до лінійної Р. Y по X 1, ..., X k, якщо покласти X k = X k.

Простим прикладом Р. Y по Х є залежність між Y і X, яка виражається співвідношенням: Y = u (X) + d, де u (x) = Е (Y I X = х), а випадкові величини Х і d незалежні. Це уявлення корисно, коли планується експеримент для вивчення функціонального зв'язку у = u (х) між невипадковими величинами у та х.

На практиці зазвичай коефіцієнти Р. в рівнянні у = u (х) невідомі і їх оцінюють за експериментальними даними (див. регресійний аналіз ).

Спочатку термін «Р.» був ужитий англійським статистиком Ф. Гальтон (1886) в теорії спадковості в наступній спеціальній сенсі: «поверненням до середнього стану» (regression to mediocrity) було названо явище, яке у тому, що діти тих батьків, зростання яких перевищує середнє значення на а одиниць, мають в середньому зростання, що перевищує середнє значення менше ніж на а одиниць.

Літ .: Крамер Г., Математичні методи статистики, пер. з англ., М., 1948; Кендалл М. Дж., Стюарт А., Статистичні висновки і зв'язку, пров. з англ., М., 1973.

А. В. Прохоров.